
20.(12分)如图10,⊙O的半径为4 cm,点P是⊙O外一点,OP=6 cm,求:
(1)以P为圆心作⊙P与⊙O外切,小圆⊙P的半径是多少?
(2)以P为圆心作⊙P与⊙O内切,大圆⊙P的半径是多少?
(分别作出图形,并解答)
19.(9分)图9是破残的圆轮片,现想把它复原成与原物大小相同的圆轮,你的方案怎样?请在图中用尺规作图补全图形.(不写作法,保留作图痕迹)




图9 图10 图11 图12
18.(10分)如图8,AB在⊙O的直径,点D在AB的延长线上,且BD=OB,点C在⊙O上,∠CAB=30°.
(1)CD是⊙O的切线吗?说明你的理由;
(2)AC=_____,请给出合理的解释.
17.(9分)已知:如图7,在△ABC中,∠BAC=120°,AB=AC,BC=4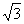 ,以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的关系如何?并证明你的结论.
,以A为圆心,2为半径作⊙A,试问:直线BC与⊙A的关系如何?并证明你的结论.
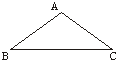
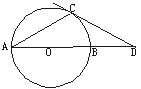
图7 图8
16.关于下列四种说法中,你认为正确的有
①圆心距小于两圆半径之和的两圆必相交 ②两个同心圆的圆心距为零? ③没有公共点的两圆必外离 ④两圆连心线的长必大于两圆半径之差
A.1个 B.2个 C.3个 D.4个
15.P是⊙O外一点,PA、PB切⊙O于点A、B,Q是优弧AB上的一点,如图6,设∠APB=α, ∠AQB=β,则α与β的关系是
A.α+β=90° B.α=β
C.α+2β=180° D.2α+β=180°
14.直线l上的一点到圆心的距离等于⊙O的半径,则l与⊙O的位置关系是
A.相离 B.相交 C.相切 D.相切或相交
13.如图5,两枚大小相同的硬币,一枚固定不动,另一枚绕其边缘滚动(无滑动),当运动硬币滚动到原来位置(第一次重合)时,运动硬币自转了______圈.
A.1 B.2 C.3 D.4

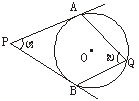
图5 图6
12.已知OA平分∠BOC,P是OA上任意一点,以P为圆心的圆与OC相切,那么⊙P与OB的位置关系是
A.相离 B.相切 C.相交 D.不能确定
11.如图4,PA切⊙O于A,AB⊥OP于B,若PO=8 cm,BO=2 cm,则PA的长为
A.16 cm B.48 cm
C.6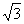 cm
D.4
cm
D.4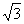 cm
cm
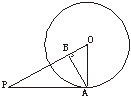
图4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com