
2.根据切线的判定,要求AE与⊙O相切,需求∠BAE=90°,由AB为
⊙O的直径得∠ACB=90°,则∠BAC+∠B=90°,所以∠CAE+∠BAC=90°,即∠BAE=90°.
[师]请大家按照我们刚才的分析写出步骤.
[生]1.解:∵∠C=90°,AC=12,BC=9,
∴由勾股定理得AB=15.
∵⊙O切AC于点E,连接OE,
∴OE⊥AC.
∴OE∥BC.∴△OAE∽△BAC.
∴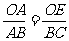 ,即
,即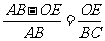 .
.
∴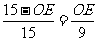 .∴OE=
.∴OE=
∴AD=AB-2OD=AB-2OE=15- ×2=
×2=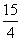 .
.
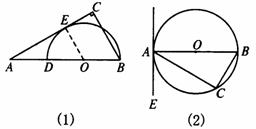
2.如图(2),AB是⊙O的直径,C是⊙O上的一点,∠CAE=∠B,你认为AE与⊙O相切吗?为什么?
分析:1.由⊙O与AC相切可知OE⊥AC,又∠C=90°,所以△AOE∽△ABC,则对应边成比例, .求出半径和OA后,由OA-OD=AD,就求出了AD.
.求出半径和OA后,由OA-OD=AD,就求出了AD.
1.如图(1),在Rt△ABC中,∠C=90°,AC=12,BC=9,D是AB上一点,以BD为直径的⊙O切AC于点E,求AD的长.
2.直线和圆的位置关系
[生]直线和圆的位置关系也有三种,即相离、相切、相交,当直线和圆有两个公共点时,此时直线与圆相交;当直线和圆有且只有一个公共点时,此时直线和圆相切;当直线和圆没有公共点时,此时直线和圆相离.
[师]总结得不错,判断一条直线和圆的位置关系有哪些方法呢?
[生]有两种方法,一种就是从公共点的个数来判断,上面已知讨论过了,另一种是比较圆心到直线的距离d与半径的大小.
当d<r时,直线和圆相交;
当d=r时,直线和圆相切;
当d>r时,直线和圆相离.
[师]很好,下面我们做一个练习.
(投影片C)
如图,点A的坐标是(-4,3),以点A为圆心,4为半径作圆,则⊙A与x轴、y轴、原点有怎样的位置关系?
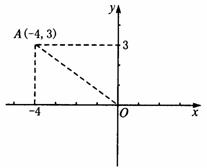
分析:因为x轴、y轴是直线,所以要判断⊙A与x轴、y轴的位置关系,即是判断直线与圆的位置关系,根据条件需用圆心A到直线的距离d与半径r比较.O是点,⊙A与原点即是求点和圆的位置关系,通过求OA与r作比较即可.
[生]解:∵A点的坐标是(-4,3),
∴A点到x轴、y轴的距离分别是3和4.
又因为⊙A的半径为4,
∴A点到x轴的距离小于半径,到y轴的距离等于半径.
∴⊙A与x轴、y轴的位置关系分别为相交、相切.
由勾股定理可求出OA的距离等于5,因为OA>4,所以点O在圆外.
[师]上面我们讨论了直线和圆的三种位置关系,下面我们要对相切这种位置关系进行深层次的研究,即切线的性质和判定.
[生]切线的性质是:圆的切线垂直于过切点的直径.
切线的判定是:经过直径的一端,并且垂直于这条直径的直线是圆的切线.
[师]下面我们看它们的应用.
(投影片D)
2.如图(2),菱形ABCD中,对角线AC和BD相交于点O,E、F、G、H分别是各边的中点.因为菱形的对角线互相垂直,所以△AOB、△BOC、△COD、△DOA都是直角三角形,又由于E、F、G、H分别是各直角三角形斜边上的中点,所以OE、OF、OG、OH分别是各直角三角形斜边上的中线,因此有OE=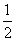 AB,OF=
AB,OF=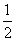 BC,OG=
BC,OG=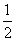 CD,OH=
CD,OH=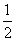 AD,而AB=BC=CD=DA.所以OE=OF=OG=OH.即各中点E、F、G、H到对角线的交点O的距离相等,所以菱形各边的中点在同一个圆上.
AD,而AB=BC=CD=DA.所以OE=OF=OG=OH.即各中点E、F、G、H到对角线的交点O的距离相等,所以菱形各边的中点在同一个圆上.
2.菱形各边的中点在同一个圆上吗?
分析:要判断某些点是否在圆上,只要看这些点到圆心的距离是否等于半径.
[生]1.解:如图(1),在Rt△OPD中,
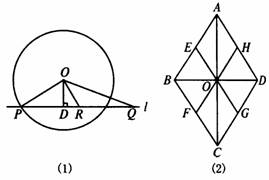
∵OD=3,PD=4,
∴OP= =5=r.
=5=r.
所以点P在圆上.
同理可知OR=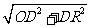 <5,OQ=
<5,OQ= >5.
>5.
所以点R在圆内,点Q在圆外.
1.⊙O的半径r=5cm,圆心O到直线l的 距离d=OD=3 m.在直线l上有P、Q、R三点,且有PD=4cm,QD>4cm,RD<4cm,P、Q、R三点对于⊙O的位置各是怎样的?
[师]我们在本章学习了三种位置关系,即点和圆的位置关系;直线和圆的位置关系;圆和圆的位置关系.下面我们逐一来回顾.
1.点和圆的位置关系
[生]点和圆的位置关系有三种,即点在圆外;点在圆上;点在圆内.判断一个点是在圆的什么部位,就是看这一点与圆心的距离和半径的大小关系,如果这个距离大于半径,说明这个点在圆外;如果这个距离等于半径,说明这个点在圆上;如果这个距离小于半径,说明这个点在圆内.
[师]总结得不错,下面看具体的例子.
(投影片B)
[师]作圆的问题实质上就是圆心和半径的问题,确定了圆心和半径,圆就随之确定.我们在探索这一问题时,与作直线类比,研究了经过一个点、两个点、三个点可以作几个圆,圆心的分布和半径的大小有什么特点.下面请大家自己总结.
[生]经过一个点可以作无数个圆.因为以这个点以外的任意一点为圆心,以这两点所连的线段为半径就可以作一个圆.由于圆心是任意的,因此这样的圆有无数个.
经过两点也可以作无数个圆.
设这两点为A、B,经过A、B两点的圆,其圆心到A、B两点的距离一定相等,所以圆心应在线段AB的垂直平分线上,在AB的垂直平分线上任意取一点为圆心,这一点到A或B的距离为半径都可以作一个经过A、B两点的圆.因此这样的圆也有无数个.
经过在同一直线上的三点不能作圆.
经过不在同一直线上的三点只能作一个圆.要作一个圆经过A、B、C三点,就要确定一个点作为圆心,使它到三点A、B、C的距离相等,到A、B两点距离相等的点在线段AB的垂直平分线上,到B、C两点距离相等的点应在线段B、C的垂直平分线上,那么同时满足到A、B、C三点距离相等的点应既在AB的垂直平分线上,又在BC的垂直平分线上,既两条直线的交点,因为交点只有一个,即确定了圆心.这个交点到A点的距离为半径,所以这样的圆只能作出一个.
[师]经过不在同一条直线上的四个点A、B、C、D能确定一个圆吗?
[生]不一定,过不在同一条直线上的三点,我们可以确定一个圆,如果另外一个点到圆心的距离等于半径,则说明四个点在同一个圆上,如果另外一个点到圆心的距离不等于半径,说明四个点不在同一个圆上.
例题讲解(投影片A)
矩形的四个顶点在以对角线的交点为圆心的同一个圆上吗?为什么?
[师]请大家互相交流.
[生]解:如图,矩形ABCD的对角线AC和BD相交于点O.
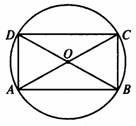
∵四边形ABCD为矩形,
∴OA=OC=OB=OD.
∴A、B、C、D四点到定点O的距离都等于矩形对角线的一半.
∴A、B、C、D四点在以O为圆心,OA为半径的圆上.
21.(12分)已知:三角形ABC内接于⊙O,过点A作直线EF.
(1)如图11,AB为直径,要使得EF是⊙O的切线,只需保证∠CAE=∠_____,并证明之;
(2)如图12,AB为⊙O非直径的弦,(1)中你所添出的条件仍成立的话,EF还是⊙O的切线吗?若是,写出证明过程;若不是,请说明理由并与同学交流.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com