
1. 能利用圆锥的侧面积公式计算实际问题
2. 圆的总复习
1. 圆锥的侧面积
3.圆和圆的位置关系
2.直线和圆的位置关系.
1.点和圆的位置关系;
2.两个同心圆中,大圆的弦AB和AC分别和小圆相切于点D和E,则DE与BC的位置关系怎样?DE与BC之间有怎样的数量关系?(DE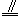
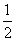 BC)
BC)
Ⅳ.课时小结
本节课巩固了如何确定圆;点和圆、直线和圆、圆和圆之间的位置关系;如何作三角形的外接圆和内切圆.
Ⅴ.课后作业
复习题 B组
Ⅵ.活动与探究
如图,⊙O是Rt△ABC的内切圆,∠ACB=90°,AB=13,AC=12,求图中阴影部分的面积.
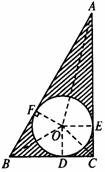
分析:根据图形,阴影部分的面积等于三角形ABC的面积与⊙O的面积差,由勾股定理可求出直角边BC的长度,则能求出S△ABC,要求圆的面积,则需求⊙O的半径OD或OE、OF.连接OA、OB、OC,则把△ABC分成三个三角形,即△OAB,△OBC、△OCA,则有S△ABC=S△OAB+S△OBC+S△OCA,从中可求出半径.
解:如图连接OA、OB、OC,则△ABC分成三个三角形,△OAB、△OBC、△OCA,OE、OF、OD分别是三角形各边上过切点的半径.
∴S△OAB=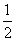 AB·OF,S△OBC=
AB·OF,S△OBC=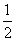 BC·OD,S△OCA=
BC·OD,S△OCA=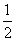 CA·OE.
CA·OE.
∵S△ABC=S△OAB+S△OBC+S△OCA,
∴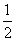 AC·BC=
AC·BC=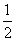 AB·OF+
AB·OF+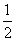 BC·OD+
BC·OD+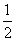 CA·OE.
CA·OE.
∵OD=OE=OF,
∴AC·BC=(AB+BC+CA)·OD.
在Rt△ABC中,AB=13,AC=12,由勾股定理得BC=5.
∴12×5=(12+13+5)·OD.
∴OD=2.
∴S阴影=S△ABC-S⊙O=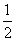 ×12×5-π·22=30-4π.
×12×5-π·22=30-4π.
板书设计
回顾与思考
[生]过不在同一条直线上的三个点可以确定一个圆,这个圆叫做三角形的外接圆,外接圆的圆心叫三角形的外心,它是三角形三边垂直平分线的交点.
因为画圆的关键是确定圆心和半径,所以作三角形的外接圆时,只要找三边垂直平分线的交点,这就是圆心,以这点到三角形任一顶点间的距离为半径就可作出三角形的外接圆.
和三角形三边都相切的圆;叫做三角形的内切圆,内切圆的圆心是三角形三条角平分线的交点,叫三角形的内心.因此,作三角形的内切圆时,只要作两条角平分线就找到了圆心,以这点与任一边之间的距离为半径,就可作出三角形的内切圆.
Ⅲ.课堂练习
1.画三个半径分别为2cm、2.5cm、4cm的圆,使它他们两两外切.
3.圆和圆的位置关系
[师]还是请大家先总结内容,再进行练习.
[生]圆和圆的位置关系有三大类,即相离、相切、相交,其中相离包括外离和内含,相切包括外切和内切,因此也可以说圆和圆的位置关系有五种,即外离、外切、相交、内切、内含.
[师]那么应根据什么条件来判断它们之间的关系呢?
[生]判断圆和圆的位置关系;是根据公共点的个数以及一个圆上的点在另一个圆的内部还是外部来判断.
当两个圆没有公共点时有两种情况,即外离和内含两种位置关系.当每个圆上的点都在另一个圆的外部时是外离;当其中一个圆上的点都在另一个圆的内部时是内含.
当两个圆有唯一公共点时,有外切和内切两种位置关系,当除公共点外,每个圆上的点都在另一个圆的外部时是外切;当除公共点外,其中一个圆上的点都在另一个圆的内部时是内切.
两个圆有两个公共点时,一个圆上的点有的在另一个圆的内部,有的在另一个圆的外部时是相交.两圆相交只要有两个公共点就可判定它们的位置关系是相交.
[师]只有这一种判定方法吗?
[生]还有用圆心距d和两圆的半径R、r之间的关系能判断外切和内切两种位置关系,当d=R+r时是外切,当d=R-r(R>r)时是内切.
[师]下面我们还可以用d与R,r的关系来讨论出另外三种两圆的位置关系,大家分别画出外离、内含和相交这三种位置关系.探索它们之间的关系,它们的关系可能是存在相等关系,也有可能是存在不等关系.(让学生探索)大家得出结论了吗?是不是这样的.
当d>R+r时,两圆外离;
当R-r<d<R+r时,两圆相交;
当d<R-r(R>r)时,两圆内含.
(投影片E)
设⊙O1和⊙O2的半径分别为R、r,圆心距为d,在下列情况下,⊙O1和⊙O2的位置关系怎样?
①R=6cm,r=3cm,d=4cm;
②R=6cm,r=3cm,d=0;
③R=3cm,r=7cm,d=4cm;
④R=1cm,r=6cm,d=7cm;
⑤R=6cm,r=3cm,d=10cm;
⑥R=5cm,r=3cm,d=3cm;
⑦R=3cm,r=5cm,d=1cm.
[生](1)∵R-r=3cm<4cm<R+r=9cm,
∴⊙O1与⊙O2的位置关系是相交;
(2)∵d<R-r,∴两圆的位置关系是内含;
(3)∵d=r-R,∴两圆的位置关系是内切;
(4)∵d=R+r,∴两圆的位置关系是外切;
(5)∵d>R+r,∴两圆的位置关系是外离;
(6)∵R-r<d<R+r,∴两圆的位置关系是相交;
(7)∵d<r-R,∴两圆的位置关系是内含.
2.解:∵AB是⊙O的直径,
∴∠ACB=90°.∴∠CAB+∠B=90°.
∴∠CAE=∠B,
∴∠CAB+∠CAE=90°,
即BA⊥AE.∵BA为⊙O的直径,
∴AE与⊙O相切.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com