
1. 在ΔABC,∠C=90°,AC=3,BC=4,点O是ΔABC的外心,现在以O为圆心,分别以2、2.5、3、为半径作⊙O,则点C与⊙O的位置关系分别是_____________.
5. 一机械零件的横截面如图所示,作⊙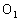 的弦AB与⊙
的弦AB与⊙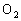 相切,且AB//
相切,且AB//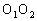 ,如果AB=10cm,则下列说法正确的是( )
,如果AB=10cm,则下列说法正确的是( )
A. 阴影面积为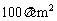 B.
阴影面积为
B.
阴影面积为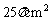
C. 阴影面积为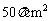 D.
因缺少数据,阴影面积无法计算
D.
因缺少数据,阴影面积无法计算

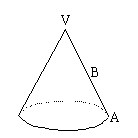
4. 如图,点B在圆锥母线VA上,且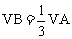 ,过点B作平行于底面的平面截得一个小圆锥,若小圆锥的侧面积为
,过点B作平行于底面的平面截得一个小圆锥,若小圆锥的侧面积为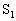 ,原圆锥的侧面积为S,则下列判断中正确的是( )
,原圆锥的侧面积为S,则下列判断中正确的是( )
A. 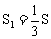 B.
B.
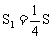 C.
C.
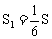 D.
D.
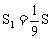
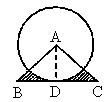
3. 如图,ΔABC为等腰直角三角形,∠A=90°,AB=AC=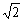 ,⊙A与BC相切,则图中阴影部分的面积为( )
,⊙A与BC相切,则图中阴影部分的面积为( )
A.  B.
B.
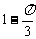 C.
C.
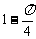 D.
D.
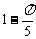
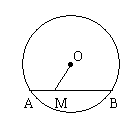
2. 如图,⊙O的直径为10厘米,弦AB的长为6cm,M是弦AB上的一动点,则线段OM的长的取值范围是( )
A. 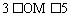 B.
B.
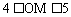
C. 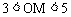 D.
D.
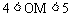
1. 下列命题中的真命题是( )
A. 三点确定一个圆 B. 平分弦的直径垂直弦
C. 圆周角等于圆心角的一半 D. 在同圆或等圆中等弧所对的圆周角相等
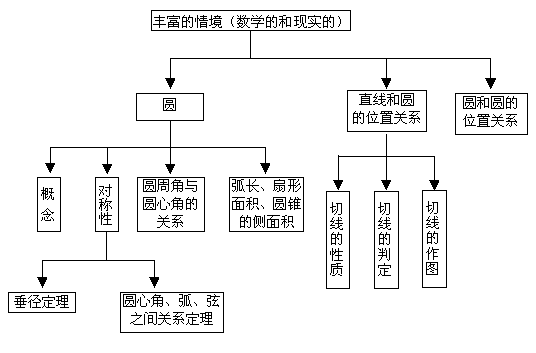
3. 本章的知识机构图
[典型例题]
例1. 已知圆锥的母线与高的夹角为30°,母线长为4cm,则它的侧面积为 cm2(结果保留π)。
答案:8π
例2. 一个扇形的弧长为4π,用它做一个圆锥的侧面,则该圆锥的底面半径为 。
答案:2
例3. 如图,矩形ABCD的长与宽分别是2cm和1cm,AB在直线l上。依次以B、C′、D″为中心将矩形ABCD按顺时针方向旋转90°,这样点A走过的曲线依次为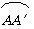 、
、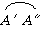 、
、 ,其中
,其中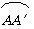 交CD于点P。
交CD于点P。

(1)求矩形A′BC′D′的对角线A′C′的长;
(2)求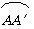 的长;
的长;
(3)求图中的 部分的面积S;
部分的面积S;
(4)求图中的 部分的面积T。
部分的面积T。
解:(1)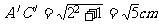
(2)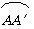 =
=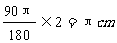 。
。
(3)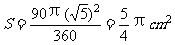 。
。
(4)连接BP,
在Rt△BCP中,BC=1,BP=2,
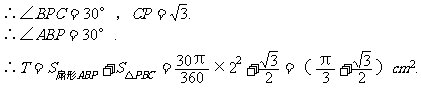
例4. 如下图,在矩形ABCD中,AD=8,点E是AB边上的一点,AE=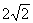 。过D、E两点作直线PQ,与BC边所在的直线MN相交于点F。
。过D、E两点作直线PQ,与BC边所在的直线MN相交于点F。
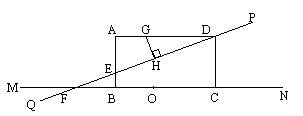
(1)求tan∠ADE的值;
(2)点G是线段AD上的一个动点(不运动至点A、D),GH⊥DE,垂足为H,设DG为x,四边形AEHG的面积为y,请求出y与x之间的函数关系式;
(3)如果AE=2EB,点O是直线MN上的一个动点,以O为圆心作圆,使⊙O与直线PQ相切,同时又与矩形ABCD的某一边相切。问满足条件的⊙O有几个?并求出其中一个圆的半径。
解:(1)∵矩形ABCD中,∠A=90°,AD=8,AE=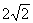
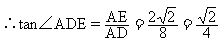
(2)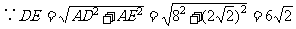 ,
,
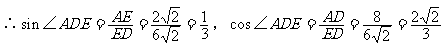
在Rt△DGH中,∵GD=x,
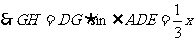
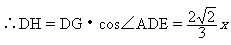 ,
,
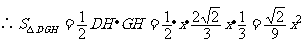
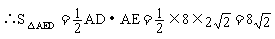
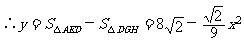
即y与x之间的函数关系式是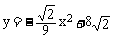 。
。
(3)满足条件的⊙O有4个。
以⊙O在AB的左侧与AB相切为例,求⊙O半径如下:
∵AD∥MN,
∴△AED∽△BEF。
∴∠PFN=∠EDA。
∴sin∠PEN=sin∠EDA=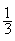 。
。
∵AE=2BE,
∴△AED与△BEF的相似比为2∶1。
∴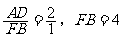 。
。
过点O作OI⊥PQ,垂足为I,设⊙O的半径为r,那么FO=4-r。
 ,
,
∴r=1。
(满足条件的⊙O还有:⊙O在AB的右侧与AB相切,这时r=2;⊙O在CD的左侧与CD相切,这时r=3;⊙O在CD的右侧与CD相切,这时r=6)
例5. 已知⊙O的半径为1,以O为原点,建立如图所示的直角坐标系。有一个正方形ABCD,顶点B的坐标为(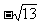 ,0),顶点A在x轴上方,顶点D在⊙O上运动。
,0),顶点A在x轴上方,顶点D在⊙O上运动。
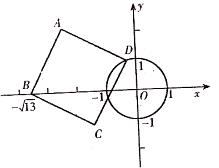
(1)当点D运动到与点A、O在一条直线上时,CD与⊙O相切吗?如果相切,请说明理由,并求出OD所在直线对应的函数表达式;如果不相切,也请说明理由。
(2)设点D的横坐标为x,正方形ABCD的面积为S,求出S与x的函数关系式,并求出S的最大值和最小值。
解:(1)CD与⊙O相切。
因为A、D、O在一直线上,∠ADC=90°,
所以∠CDO=90°,所以CD是⊙O的切线。
CD与⊙O相切时,有两种情况:
①切点在第二象限时(如图①),
设正方形ABCD的边长为a,则a2+(a+1)2=13.
解得a=2,或a=-3(舍去)。
过点D作DE⊥OB于E,
则Rt△ODE∽Rt△OBA,
所以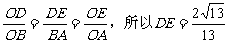 。
。
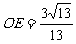 ,所以点D1的坐标是(
,所以点D1的坐标是( ),
),
所以OD所在直线对应的函数表达式为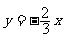 。
。
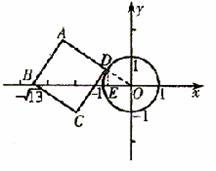
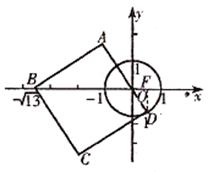
图① 图②
②切点在第四象限时(如图②),
设正方形ABCD的边长为b,则b2+(b-1)2=13,
解得b=-2(舍去),或b=3。
过点D作DF⊥OB于F,则Rt△ODF∽Rt△OBA,
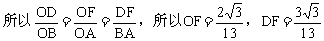
所以点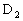 的坐标是
的坐标是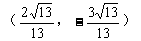
所以OD所在直线对应的函数表达式为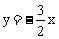
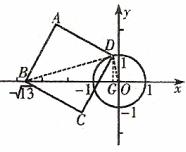
图 ③
(2)如图③,过点D作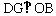 于G,连接BD、OD,则
于G,连接BD、OD,则
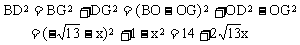
所以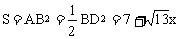 。
。
因为-1≤x≤1,所以S的最大值为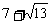 ,S的最小值为
,S的最小值为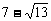 。
。
例6. 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm。半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm。
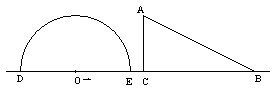
(1)当t为何值时,△ABC的一边所在的直线与半圆O所在的圆相切?
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,如果半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分,求重叠部分的面积。
解:(1)①如图1,当点E与点C重合时,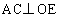 ,OC=OE=6cm,所以AC与半圆O所在的圆相切。此时点O运动了2cm,所求运动时间为:
,OC=OE=6cm,所以AC与半圆O所在的圆相切。此时点O运动了2cm,所求运动时间为: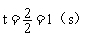 。
。
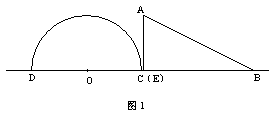
②如图2,当点O运动到点C时,过点O作OF⊥AB,垂足为F。
在Rt△FOB中,∠FBO=30°,OB=12cm,则OF=6cm,即OF等于半圆O的半径,所以AB与半圆O所在的圆相切。此时点O运动了8cm,所求运动时间为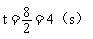 。
。
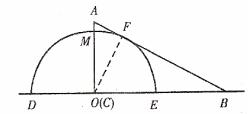
图 2
③如图3,当点O运动到BC的中点时,AC⊥OD,OC=OD=6cm,所以AC与半圆O所在的圆相切,此时点O运动了14cm,所求运动时间为: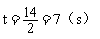 。
。
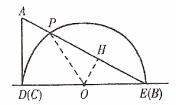
图 3
④如图4,当点O运动到B点的右侧,且OB=12cm时,过点O作OQ⊥直线AB,垂足为Q。
在Rt△QOB中,∠OBQ=30°,
则OQ=6cm,即OQ等于半圆O所在的圆的半径,
所以,直线AB与半圆O所在的圆相切,此时点O运动了32cm,所求运动时间为: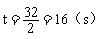 。
。
因为半圆O在运动中,它所在的圆与AC所在的直线相切只有上述①、③两种情形;与AB所在的直线相切只有上述②、④两种情形;与BC所在直线始终相交。所以只有当t为1s,4s,7s,16s时,△ABC的一边所在的直线与半圆O所在的圆相切。
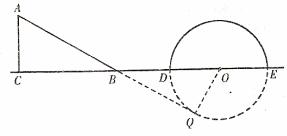
图4
(2)当△ABC的一边所在的直线与半圆O所在的圆相切时,半圆O与直径DE围成的区域与△ABC三边围成的区域有重叠部分的只有如图2与图3所示的两种情形。
①如图2,设OA与半圆O的交点为M,易知重叠部分是圆心角为90°,半径为6cm的扇形,所求重叠部分面积为:
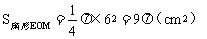 。
。
②如图3,设AB与半圆O的交点为P,连接OP,过点O作OH⊥AB,垂足为H。则PH=BH。在Rt△OBH中。
∠OBH=30°,OB=6cm,则OH=3cm,
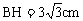 ,
,
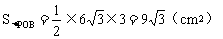 ,
,
又因为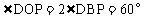 ,
,
所以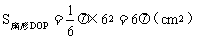 。
。
所求重叠部分面积为:
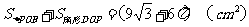 。
。
[模拟试题](答题时间:60分钟)
2. 圆锥的侧面积与底面积之和称为圆锥的全面积
知识要点:
1. 圆锥的侧面展开图是一个扇形,设圆锥的母线长为l,底面圆的半径为r,那么这个扇形的半径为l,扇形的弧长为2πr,圆锥的侧面积为πrl。
2. 灵活运用本章的知识解决综合问题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com