[生]垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧．

逆定理：平分弦(不是直径)的直径垂直于弦，并且平分弦所对的弧．

[师]这两个定理大家一定要弄清楚、不能混淆，所以我们应先对他们进行区分．每个定理都是一个命题，每个命题都有条件和结论．在垂径定理中，条件是：一条直径垂直于一条弦，结论是：这条直径平分这条弦，且平分弦所对的弧(有两对弧相等)．在逆定理中，条件是：一条直径平分一条弦(不是直径)，结论是：这条直径垂直于这条弦，并且平分弦所对的弧(也有两对弧相等)．从上面的分析可知，垂径定理中的条件是逆定理中的结论，垂径定理中的一个结论是逆定理中的条件，在具体的运用中，是根据已知条件提供的信息来决定用垂径定理还是其逆定理，若已知直径垂直于弦，则用垂径定理；若已知直径平分弦，则用逆定理．下面我们就用一些具体例子来区别它们．

(投影片B)

1．如图(1)，在⊙O中，AB、AC为互相垂直的两条相等的弦，OD⊥AB，OE⊥AC，D、E为垂足，则四边形ADOE是正方形吗？请说明理由．

[生]圆是平面上到定点的距离等于定长的所有点组成的图形．定点为圆心，定长为半径．

圆既是轴对称图形，又是中心对称图形，对称轴是任意一条过圆心的直线，对称中心是圆心，圆还具有旋转不变性．

[师]圆的这些性质在日常生活中有哪些应用呢？你能举出例子吗？

[生]车轮做成圆形的就是利用了圆的旋转不变性．车轮在平坦的地面上行驶时，它与地面线相切，当它向前滚动时，轮子的中心与地面的距离总是不变的，这个距离就是半径．把车厢装在过轮子中心的车轴上，则车辆在平坦的公路上行驶时，人坐在车厢里会感觉非常平稳．如果车轮不是圆形，坐在车上的人会觉得非常颠．

4. 如图，⊙O的半径OC与直径AB垂直，点P在OB上运动(点O、B除外)，CP的延长线交⊙O于点D，在OB的延长线上取点E，使ED＝EP．

　　　 (1)求证：ED是⊙O的切线；

　　　 (2)当OC＝2，ED＝2时，求∠E的正切值tanE和图中阴影部分的面积．

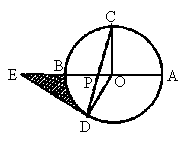
3. 如图，OA、OB是⊙O的两条半径，且OA⊥OB，点C是OB延长线上任意一点，过点C作CD切⊙O于点D，连接AD交OC于点E．求证：CD＝CE；

　　　 (1)若将图(a)中的半径OB所在的直线向上平移交OA于F，交⊙O于B'，其他条件不变(如图(b))，那么上述结论CD＝CE还成立吗？为什么？

　　　 (2)若将图(a)中的半径OB所在直线向上平行移动到⊙O外的CF，点E是DA的延长线与CF的交点，其他条件不变(如图(c))，那么上述结论CD＝CE还成立吗？为什么？

2. 如图，已知BC是⊙O的直径，AH⊥BC，垂足为D，点A为弧BF的中点，BF交AD于E，且，AD＝6，

　　　 (1)求证：AE＝BE；

　　　 (2)求DE的长；

　　　 (3)求BD的长．

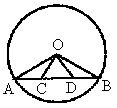
1. 已知：如图，在⊙O中，AB为弦，C、D两点在AB上，且AC＝BD，请你仔细观察后回答：图中共有几个等腰三角形？把它们分别写出来，并说明你的理由．

5. 如图，四边形ABCD是正方形，曲线叫做“正方形的渐开线”，其中弧、弧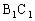、弧、弧…的圆心依次按A、B、C、D循环，它依次连接，取AB＝1，则曲线的长是___________．

4. 把一个半径为12厘米的圆片，剪去一个圆心角为120°的扇形后，用剩下的部分做成一个圆锥侧面，那么这个圆锥的侧面积是___________．

3. 在RtΔABC，斜边AB＝13cm，BC＝12cm，以AB的中点O为圆心，2.5cm为半径画圆，则直线BC和⊙O的位置关系是________________．

2. 如图在⊙O中，直径AB⊥弦CD，垂足为P，∠BAD＝30°，则∠AOC的度数是________度．