
1.如图3-29所示,若AC、BD、EF两两互相平分于点O,则图中共有平行四边形 个;
5.弧长、扇形面积、圆锥的侧面积和全面积.
4.圆心角与圆周角的关系;
3.圆心角、弧、弦之间关系定理;
2.垂径定理及其逆定理;
[师]我们经过探索,归纳出弧长、扇形面积、圆锥的侧面积公式,大家不仅要牢记公式,而且要把它的由来表述清楚,由于时间关系,我们在这里不推导公式的由来,只是让学生掌握公式并能运用.
[生]弧长公式l=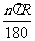 ,π是圆心角,R为半径.
,π是圆心角,R为半径.
扇形面积公式S=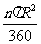 或S=
或S=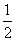 lR.n为圆心角,R为扇形的半径,l为扇形弧长.
lR.n为圆心角,R为扇形的半径,l为扇形弧长.
圆锥的侧面积S侧=πrl,其中l为圆锥的母线长,r为底面圆的半径.
S全=S侧+S底=πrl+πr2.
Ⅲ.课时小结
本节课我们复习巩固了圆的概念及对称性;垂径定理及其逆定理;圆心角、弧、弦、弦心距之间的关系;圆心角和圆周角的关系;弧长、扇形面积、圆锥的侧面积和全面积.
Ⅳ.课后作业
复习题 A组
Ⅴ.活动与深究
弓形面积
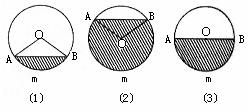
如图,把扇形OAmB的面积以及△OAB的面积计算出来,就可以得到弓形AmB的面积.如图(1)中,弓形AmB的面积小于半圆的面积,这时S弓形=S扇形-S△OAB;图(2)中,弓形AmB的面积大于半圆的面积,这时S弓形=S扇形+S△OAB;图(3)中,弓形AmB的面积等于半圆的面积,这时S弓形=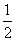 S圆.
S圆.
例题:水平放着的圆柱形排水管的截面半径是0.6m,其中水面高是0.3m,求截面上有水的弓形的面积(精确到0.01m2).
解:如图,在⊙O中,连接OA、OB,作弦AB的垂直平分线,垂足为D,交 于点C.
于点C.
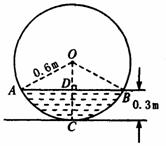
∵OA=0.6,DC=0.3,
∴OD=0.6-0.3=0.3,∠AOD=60°,AD=0.3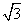 .
.
∵S弓形ACB=S扇形OACB-S△OAB,
∴S扇形OACB=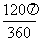 ·0.62=0.12π(m2),
·0.62=0.12π(m2),
S△OAB=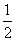 AB·OD=
AB·OD=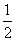 ×0.6
×0.6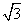 ×0.3=0.09
×0.3=0.09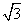 (m2)
(m2)
∴S弓形ACB=0.12π-0.09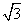 ≈0.22(m2).
≈0.22(m2).
板书设计
回顾与思考
[生]一条弧所对的圆周角等于它所对的圆心角的一半.
在同圆或等圆中,同弧或等弧所对的圆周角相等.
直径所对的圆周角是直角,90°的圆周角所对的弦是直径.
[师]大家先回忆一下本部分内容.
[生]在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量都分别相等.
[师]下面我们进行有关练习
(投影片C)
1.如图在⊙O中,弦AB所对的劣弧为圆的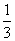 ,圆的半径为2cm,求AB的长.
,圆的半径为2cm,求AB的长.
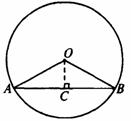
[生]解:由题意可知 的度数为120°,
的度数为120°,
∴∠AOB=120°.
作OC⊥AB,垂足为C,则
∠AOC=60°,AC=BC.
在Rt△ABC中,
AC=OAsin60°=2×sin60°=2×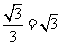 .
.
∴AB=2AC=2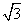 (cm).
(cm).
2.解:∵C为AB的中点,
∴OC⊥AB,
在Rt△OAC中,AC=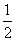 AB=25mm,OA=50mm.
AB=25mm,OA=50mm.
∴由勾股定理得OC=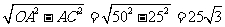 (mm).
(mm).
2.如图(2),在⊙O中,半径为50mm,有长50mm的弦AB,C为AB的中点,则OC垂 直于AB吗?OC的长度是多少?
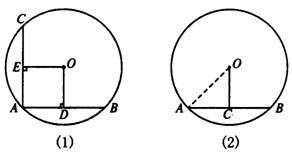
[师]在上面的两个题中,大家能分析一下应该用垂径定理呢,还是用逆定理呢?
[生]在第1题中,OD、OE都是过圆心的,又OD⊥AB、OE⊥AC,所以已知条件是直径垂直于弦,应用垂径定理;在第2题中,C是弦AB的中点,因此已知条件是平分弦(不是直径)的直径,应用逆定理.
[师]很好,在家能用这两个定理完成这两个题吗?
[生]1.解:∵OD⊥AB,OE⊥AC,AB⊥AC,
∴四边形ADOE是矩形.
∵AC=AB,∴AE=AD.
∴四边形ADOE是正方形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com