5．“利海”通讯器材市场，计划用60000元从厂家购进若干部新型手机，以满足市场需求．已知该厂家生产三种不一同型号的手机，出厂价分别为甲种型号手机每部1800元，乙种型号手机每部600元，丙种型号手机每部1200元．

(1)若商场同时购进其中两种不同型号的手机共40部，并将60000元恰好用完．请你帮助商场计算一下如何购买？

(2)若商场同时购进三种不同型号的手机共40部，并将60000元恰好用完，并且要求乙种型号的手机购买数量不少于6部且不多于8部，请你求出每种型号手机的购买数量．

4．某学校社会实践小分队走访100户家庭，发现一般洗衣水的浓度以0．2%-0．5%为合适，即100kg洗衣水里含200-500g的洗衣粉比较合适，因为这时表面活性最大，去污效果最好．现有一个洗衣缸可容纳15kg洗衣水(包括衣服)，已知缸中的已有衣服重4kg，所需洗衣水的浓度为0．4%，已放了两匙洗衣粉(1匙洗衣粉约为0．02kg)问还需加多少kg洗衣粉，添多少kg水比较合适？

3．牛奶和鸡蛋所含各种主要成分的百分比如下表．又知每1g蛋白质、脂肪、碳水化合物产生和热量分别为16．8J、37．8J、16．8J．当牛奶和鸡蛋各取几克时，使它们质量之比为3：2，且产生1260J的热量？

2．先读懂古诗，然后回答诗中问题．

巍巍古寺在山林，不知寺内几多僧．

三百六十四只碗，看看用尽不差争．

三人共食一碗饭，四人共吃一碗羹．

请问先生明算者，算来寺内几多僧．

1．甲、乙两汽车，甲从A地去B地，乙从B地去A地，同时相向而行，1．5小时后两车相遇．相遇后，甲车还需要2小时到达B地，乙车还需要小时到达A地．若A、B两地相距210千米，试求甲乙两车的速度．

23、如图，已知：正方形ABCD的对角线AC、BD相交于点O，BE平分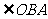，OFBE于F，交OB于G。

①　　 求证：OE=OF。

②若E在O、A两点之间运动(不与O、A重合)，OF保持与BE的垂直关系，那么OE与OG还相等吗？(不需要证明)

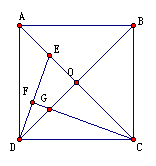
22、如图，平行四边形ABCD中，E、F分别为对角线BD上的点，且BF=DE。求证：四边形AECF是平行四边形。

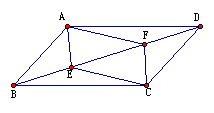
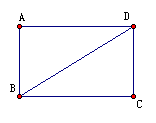
21、如图，矩形ABCD中，BD=2AB。

⑴求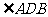的度数；

⑵若AD=3cm，求矩形ABCD的面积。

20、已知：四边形ABCD是　　　 ，E、F、G、H分别是AB、BC、CD、DA的中点，求证：四边形EFGH是　　　 。

题目中的“　　　 ”中的部分，是小明在抄题时，不小心被墨水污染无法看得清的部分，请你先在污染处填上合理的内容，并画图证明。

19、定理证明

这一章我们学习了很多定理，并对他们进行了证明，你还记得“三角形中位线定理”吗？请你先默写“三角形中位线定理”并证明这一定理。(画出图形，写出已知、求证和证明)