
(三)应用
㈠ 要使下列各式有意义,求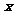 的取值范围:
的取值范围:
① 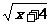 ②
②
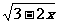 ③
③ ④
④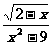
解题思路:二次根号有意义,被开方数应________
 一元一次不等式
一元一次不等式
分式有意义,分母___________
㈡ 填空
适合不等式 x>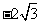 的负整数解是________________
的负整数解是________________
适合不等式 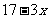 ≥2的正整数解是________________
≥2的正整数解是________________
适合不等式 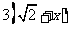 >2x的最小负整数解是________________
>2x的最小负整数解是________________
适合不等式 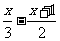 >-1的非负整数解是 ________________
>-1的非负整数解是 ________________
㈢ (1)当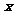 为何值时,
为何值时,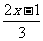 与
与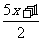 的差不大于1?
的差不大于1?
(2)求出不等式 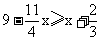 的正整数解。
的正整数解。
9.5用一元一次不等式解决问题
学习目标:
1、会解一元一次不等式的应用题。
2、进一步学习和体会转化思想在解题中的作用。
重点、难点:
挖掘题目中的不等的数量关系,列出不等式。
学习过程:
(二)巩固:改正下列各题中的错误:
⑴ 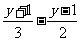 >
>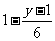 去分母 得
去分母 得
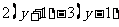 >
>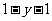
__________________________________
⑵ 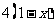 >
>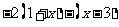 去括号
得
去括号
得
 >
>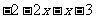
_________________________________
⑶ 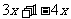 ≤
≤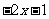 移项 得
移项 得
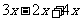 ≤
≤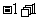
_______________________
⑷  ≥
≥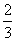 ,两边同除以
,两边同除以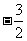 ,得 x≥
,得 x≥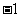
___________________________________________
(一)复习:解一元一次不等式的一般步骤:
①_____________②______________ ③______________ ④______________⑤________________
练习:解下列不等式
⑴
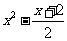 <
<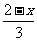 ⑵
⑵ 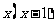 ≥
≥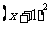
①解一元一次不等式的步骤中的去分母和未知数的系数化1这两步,若乘数或除数是负数,要改变不等号的方向;②一元一次不等式的解集中含有无限多个数;③在解题过程中,要避免解方程中易出现的错误在解不等式中重犯;④对于一元一次不等式的解法步骤,在解题时,要做到灵活运用.
(二)应用、探究
解不等式
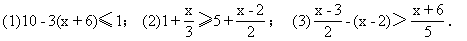
(4)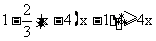 (5) ax- 8<-2x+a(a+2≠0).
(5) ax- 8<-2x+a(a+2≠0).
(一)自学、相信自己
例1:下面各题解法对不对?用“曲线”标出来,最后说明错误的原因.
(1)8x-5>4x-6.
解法一: 解法二:
8x+4x>-5-6, 6-5>4x-8x,
12x>-11, 1>-4x,
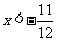
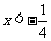
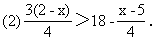
解法一:3(2-x)>18-x-5,
6-x>13-x,
x-x>13-6,
0>7.
解法二:3(2-x)>72-(x- 5),
6-3x>72-x+5,
x-3x>72+5-6,
2x>71,
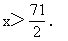
例2 解关于x的不等式:
(1)5x+1≤3x- 7; (2)4(x- 3)≤7(x- 3);
(3)8(1- y)>5(4-y)+3; (4)y-0.5(1-y)<1.6(0.3-2y);
2.说出解下列不等式并说出变形是根据不等式的哪一条性质.
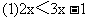
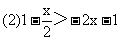
自学课本131---136页,写下疑惑摘要:
________________________________________________________________________________________________________________________________________________
1、说出解一元一次不等式的一般步骤及注意事项.
________________________________________________________________________________________________________________________________________________
2.培养学生观察、比较的能力和对不等式变形的能力.
学习重点:
掌握解法步骤并准确,熟练地求出解集.
学习难点:
正确地运用不等式基本性质2,克服变形中常犯的错误.
学习过程:
1.使学生正确运用不等式的基本性质,熟练地解一元一次不等式;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com