
(1)恩格尔系数表示家庭日常饮食开支占家庭经济总收入的比例,它反映了居民家庭的实际生活水平,各种类型家庭的恩格尔系数如下表所示:
|
家庭类型 |
贫困家庭 |
温饱家庭 |
小康家庭 |
发达国家家庭 |
最富裕国家家庭 |
|
恩格尔系数(n) |
75%以上 |
50%-75% |
40%-49% |
20%-39% |
不到 20% |
则用含n的不等式表示小康家庭的恩格尔系数为
(2)某工人计划在15天里加工408个零件,最初三天中每天加工24个,以后每天至少加工多少个零件才能在规定时间内超额完成任务。
(3)某化工厂 2003 年12月在制定 2004 年某种化肥的生产计划时,已有如下数据: ①生产该种化肥的工人不能超过200人;②每个工人全年工时不多于2100个;③预计2004年可销售80000袋;④生产一袋化肥需要工时4个;⑤每袋化肥需原料20千克;⑥库存原料800吨,本月需用200吨,2004年可补充1200吨。根据以上数据确定生产化肥袋数的范围。
(4)已知不等式组
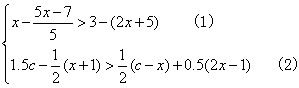
① c取何值时,只有一个整数解;②c取何值时,没有整数解.
(5)建网就等于建一所学校,哈市慧明中学,为加强现代信息技术教学,拟投资建一个初级计算机房和一个高级计算机房,每个机房只配置 1 台教师用机,若干台学生用机。其中初级机房教师用机每台 8000 元,学生用机每台 3500 元,高级机房教师用机每台 11500 元,学生用机每台 7000 元,已知两机房购买机算机的总数相等,且每个机房购买计算机的总钱数不少于 20 万元,也不超过 21 万元,则该校拟建的初级机房、高级机房各应有多少台计算机?
(1)本节解决了列一元一次不等式组解应用题,解题步骤与列方程解应用题类似,但又有区别。
(2)采用“转化” 思想,把未知问题转化为熟悉的已知问题。
(3)对材料、方法等作选择的一类应用题,应注意怎样取舍。
(4)要对例题和练习总结此类题型的解法,学用类比思想。
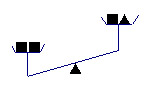
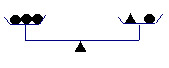
例1:设“●”、“▲”、“■”表示三个不同的物体,用天平比较它们质量的大小,两次情况如图所示, 那么 ●、▲、■这三个物体从大到小的顺序排列应为___________________
 例2:一个长方形足球场的长为米,宽为70m。如果它的周长大于350m,面积小于7560 m,求x的取值 范围,并判断这个球场是否可以用作国际足球比赛。
(注:用于国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间)
例2:一个长方形足球场的长为米,宽为70m。如果它的周长大于350m,面积小于7560 m,求x的取值 范围,并判断这个球场是否可以用作国际足球比赛。
(注:用于国际比赛的足球场的长在100m到110m之间,宽在64m到75m之间)
例3:某蔬菜生产基地计划由25个劳力承包60亩地,种甲、乙、丙三种不同的蔬菜,规定每个劳力只种一种,且甲种蔬菜必种,经测算,这些不同的蔬菜每亩所需的劳动力和预计产值如下表:
|
蔬菜品种 |
甲 |
乙 |
丙 |
|
劳动力/亩(人) |
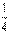 |
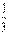 |
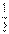 |
|
产值/亩(万元) |
0.2 |
0.3 |
0.4 |
应怎样安排才能使每亩地都能种上蔬菜,所有劳动力都有工作,且预计总产值最高?最高总产值是多少?
例4:某工厂有甲种原料630千克、乙中原料290千克,计划利用这两种原料生产A、B两种产品共50件,已知生产1件A种产品,需要甲种原料9千克、乙种原料3千克;生产1件B种产品,需要甲种原料4千克、乙种原料10千克。按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出。
3、我国个人所得税法规定,公民全月的工资、薪金收入不超过 800元的部分不必纳税;超过800元的部分为全月应纳税所得额(应该纳税的工资、薪金收入),此项税款按下表分段累进计算:
|
全月应纳税所得额 |
税率(%) |
|
不超过500元的部分 |
5 |
|
超过 500 元至
2000 元的部分 |
10 |
|
超过 2000 元至
5000 元的部分 |
15 |
|
...... |
....... |
某人1月份应缴纳此项税款 26.78 元,则他的当月工资、薪金所得介于什么范围?
2、已知不等式组
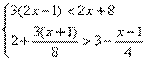
⑴ 求此不等式组的整数解;
⑵ 若上述整数解满足方程ax + 2a = x- 6 ,求 a 的值
1、把一堆苹果分给几个小孩,如果每人分3个,则剩余8个,如果前面每人分5个,则最后一个人得到的苹果数不足3个,求小孩子的人数和苹果的个数。
2、进一步学习和体会转化思想在解题中的作用。
重点、难点:
挖掘题目中的不等的数量关系,列出不等式(组)。
学习过程:
1、会用一元一次不等式组解应用题,知道步骤;
9.6一元一次不等式组 (2)
学习目标:
3.一元一次不等式组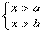 (
(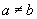 )的解集为
)的解集为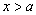 ,则
,则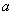 与
与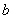 的大小关系为____________.
的大小关系为____________.
2 解不等式组:
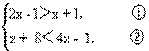
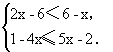
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com