
3.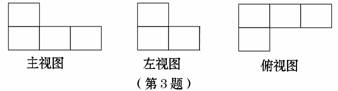 下图是由一些相同的小正方形构成的几何体的三视图,这些相同的小正方形的个数是( )
下图是由一些相同的小正方形构成的几何体的三视图,这些相同的小正方形的个数是( )
(A)4个. (B)5个. (C)6个. (D)7个.
2.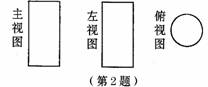 某物体三视图如图,则该物体形状可能是 ( )
某物体三视图如图,则该物体形状可能是 ( )
(A)长方体.
(B)圆锥体.
(C)立方体.
(D)圆柱体.
1. 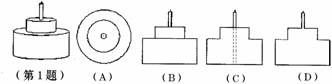 小琳过14周岁生日,父母为她预定的生日蛋糕如图所示,它的主视图应该是 ( )
小琳过14周岁生日,父母为她预定的生日蛋糕如图所示,它的主视图应该是 ( )
本节课帮助学生整合本章知识体系,使学生能运用数形结合思想,根据反比例函数的性质,解决实际问题。
 某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20米和11米的矩形大厅内修建一个60平方米的矩形健身房ABCD. 该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/平方米,新建(含装修)墙壁的费用为80元/平方米. 设健身房的高为3米,一面旧墙壁AB的长为x米,修建健身房的总投入为y元.
某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20米和11米的矩形大厅内修建一个60平方米的矩形健身房ABCD. 该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为20元/平方米,新建(含装修)墙壁的费用为80元/平方米. 设健身房的高为3米,一面旧墙壁AB的长为x米,修建健身房的总投入为y元.
(1)求y与x的函数关系式;
(2)为了合理利用大厅,要求自变量x必须满足8≤x≤12. 当投入资金为4800元时,问利用旧墙壁的总长度为多少米?
例1、如果函数 是反比例函数,那么
是反比例函数,那么 ____________.
____________.
例2、若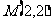 和
和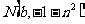 是反比例函数
是反比例函数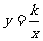 图象上的两点,则一次函数
图象上的两点,则一次函数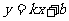 的图象经过_____________象限。
的图象经过_____________象限。
例3、已知一次函数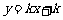 的图象与反比例函数
的图象与反比例函数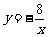 的图象在第一象限交于点
的图象在第一象限交于点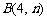 ,求k,n的值.
,求k,n的值.
例4、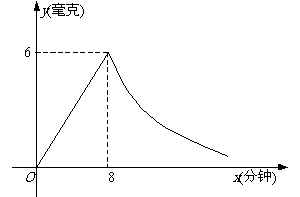 为了预防“非典”,某学校对教室采用药熏消毒法进行消毒. 已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示). 现测得药物8分钟燃毕,此时室内空气中每立方米含药量为6毫克. 请根据题中所提供的信息,解答下列问题:
为了预防“非典”,某学校对教室采用药熏消毒法进行消毒. 已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示). 现测得药物8分钟燃毕,此时室内空气中每立方米含药量为6毫克. 请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,y关于x的函数关系式为:___________________,自变量x的取值范围是:______________;药物燃烧后y关于x的函数关系式为:___________________;
(2)研究表明,当空气中每立方米的含药量低于1.6毫克时学生方可进教室,那么从消毒开始,至少需要经过几分钟后,学生才能回到教室;
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时才能有效地杀灭空气中的病菌,那么此次消毒是否有效?为什么?
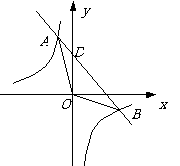 例5、如图,反比例函数
例5、如图,反比例函数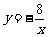 与一次函数
与一次函数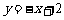 的图象交于A、B两点.
的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)求△AOB的面积.
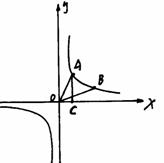 例6、如图所示,点A、B在反比例函数
例6、如图所示,点A、B在反比例函数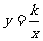 的图象上,且点A、B的横坐标分别为
的图象上,且点A、B的横坐标分别为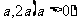 。
。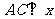 轴,垂足为C,且
轴,垂足为C,且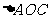 的面积为2。
的面积为2。
⑴求该反比例函数的解析式。
⑵若点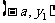 、
、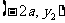 在该反比例函数的图象上,试比较
在该反比例函数的图象上,试比较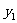 与
与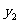 的大小。
的大小。
⑶求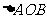 的面积。
的面积。
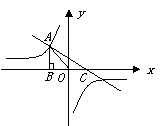 (06成都)如图,已知反比例函数
(06成都)如图,已知反比例函数 的图象经过点
的图象经过点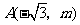 ,过点
,过点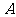 作
作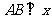 轴于点
轴于点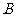 ,且
,且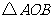 的面积为
的面积为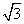 .求
.求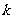 和
和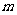 的值.
的值.
10.[06常州]如图,△POA1,△P2A1A2,△P3A2A3,……,△PnAn-1An都是等腰直角三角形,点P1,P2,P3,……,Pn在函数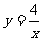 (x>0)的图象上,斜边OA1,A1A2,A2A3,……,An-1An都在x轴上,则点A1的坐标是___________,点A2的坐标是__________,点A2006的坐标是_______.
(x>0)的图象上,斜边OA1,A1A2,A2A3,……,An-1An都在x轴上,则点A1的坐标是___________,点A2的坐标是__________,点A2006的坐标是_______.
9.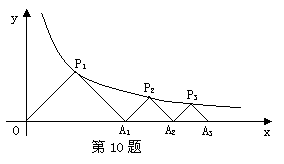 [05浙江]两个反比例函数
[05浙江]两个反比例函数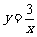 ,
,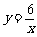 在第一象限内的图象如图所示, 点P1,P2,P3,…,P2 007在反比例函数
在第一象限内的图象如图所示, 点P1,P2,P3,…,P2 007在反比例函数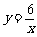 图象上,它们的横坐标分别是x1,x2,x3,…,x2 007,纵坐标分别是1,3,5,…,共2007个连续奇数,过点P1, P2,P3,…,P2 005分别作y轴的平行线,与
图象上,它们的横坐标分别是x1,x2,x3,…,x2 007,纵坐标分别是1,3,5,…,共2007个连续奇数,过点P1, P2,P3,…,P2 005分别作y轴的平行线,与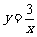 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2 007(x2 007,y2 007),则 y2 007=________________.
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2 007(x2 007,y2 007),则 y2 007=________________.
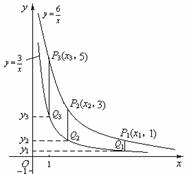 (9题图)
(9题图)
8.[05北京] 如果反比例函数的图象经过点(1,-2),那么这个反比例函数的解析式为_______________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com