
2、例题
例1 (P166例1)
求单项式5x2y,-2 x2y,2xy2,-4xy2的和。
分析:式子5x2y+(-2 x2y)+2xy2+(-4xy2)就是这四个单项式的和。几个整式相加减,通常用括号把每一个整式括号起来,再用加减号连接。
解:(略,见教材P166)
例2(P166例2)
求3x2-6x+5与4x2-7x-6的和。
解:(3x2-6x+5)+(4x2-7x-6) (每个多项式要加括号)
=3x2-6x+5+4x2-7x-6 (去括号)
=7x2+x-1 (合并同类项)
例3。(P166例3)
求2x2+xy+3y2与x2-xy+2y2的差。
解:(2x2+xy+3y2)-( x2-xy+2y2)
=2x2+xy+3y2-x2+xy-2y2
=x2+2xy+y2
1、引入
整式的化简,如果有括号,首先要去括号,然后合并同类项,所以去括号和合并同类项是整式加减的基础。
3、化简:
y2+(x2+2xy-3y2)-(2x2-xy-2y2)
2、叙述去括号与添括号法则。
1、叙述合并同类项法则。
3、分析:注意指导学生写出y与x之间的关系
当0<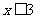 时 y = 8
时 y = 8
当 x>3时 y=1.5(x-3)+ 8=1.5x+3.5
2、解:甲旅行团成人的门票费用为15x元,
儿童的门票费用为:7.5y元。
总和是(15x+7.5y) 元
乙旅行团成人数为:2x
门票费用为:30x元,
儿童人数为:(2y-8)
门票费用为:7.5(2y-8)元。
总和是[30x+7.5(2y-8)]元
即(30x+15y-60)元
|
问题与情景 |
师生行为 |
设计意图 |
|
|
一、创设情景,提出问题 (课件显示)动物们要举行庆祝大会,兔妈妈受到邀请,准备了一个合唱的节目,兔妈妈想这样安排,第一排站n只兔子,从第二排起每排都比前一排多一只兔子,一共站了四排,请你帮它算一下兔妈妈一共需要多少只兔子? 课件显示课题。 |
教师课前准备时展示幻灯片,呈现问题,引入复习主题。 学生独立完成: 第一排:n 只 第二排:(n+1)只 第三排:(n+2)只 第四排: (n+3)只 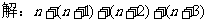  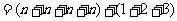 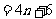 答:一共需要(4n+6)只兔子 教师给出本节课题 |
通过这个生动的例子有效地吸引学生的注意力,增强学生的好奇心和求知欲,激发学习的积极性。 例子中涉及到用字母表示数,列代数式,去括号,合并同类项等内容,由此自然引入到本课内容。 |
|
|
二、知识点回顾 课件显示: [知识结构总结]
|
教师注意利用知识结构图引导学生回顾本章主要内容并适当总结。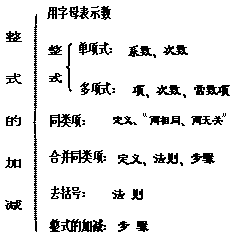
|
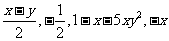
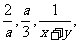 1、在式子:
1、在式子: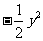 中,哪些是单项式,哪些是多项式?哪些是整式?
中,哪些是单项式,哪些是多项式?哪些是整式?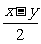 2、
的系数是( ),次数是( ),
2、
的系数是( ),次数是( ),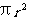 的系数是( ),次数是( );
的系数是( ),次数是( );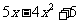
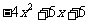
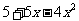
 例题(练习)
例题(练习)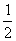
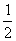
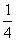 (-4x2 +2x -8) - (x-2)其中x=
(-4x2 +2x -8) - (x-2)其中x=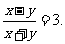
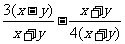 的值。
的值。 课后 应用思考:
课后 应用思考: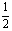
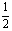 2、原式=-x2+ x-2- x+1
2、原式=-x2+ x-2- x+1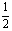 =-x2-1
=-x2-1
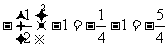
小组讨论,得出结果。
1、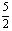 解:长方形的面积为:8x cm2
解:长方形的面积为:8x cm2
梯形的面积为: (x+3x)=10x cm2
因为 x 是正数,所以 10x>8x
所以 梯形的面积比长方形的面积大
10x-8x=2x
即 梯形的面积比长方形的面积大2x cm2
教师点评,注意提醒学生书写格式。
七年级一班学生的数学知识基础有明显的两级分化现象,处于中间位置的学生不多,有近十名学生基础知识不扎实。部分男生还没有形成较好的学习习惯,学习不够积极。
上课时善于动脑,积极发言,平时又乐于帮助同学,学习成绩优秀的占班级总人数的近一半,是这个集体的主体力量。他们学习态度端正,学习习惯较好,团结同学,不仅能较好地完成老师布置的教学任务,还能和后进生结对,解决他们在学习上的困难。还有一部分喜欢表现自己,敢于发表自己的观点,好争辩,但仍然需要在课堂活动中加以正确的引导和培养。
以小组合作为基础,通过具体的题目中让学生复习本章书的知识要点,回顾典型题目,进一步巩固和加深对知识的理解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com