1、反比例函数的性质2、综合反比例函数的知识解决综合问题

4、学会用数学语言与同伴交流，能阐述自己的观点。力争使自己由“会做”向“会讲”转变。

3、了解用“数形结合”的思想与方法解决数学问题。

2、能在实际问题中建立反比例函数模型，进而解决问题

1、会根据反比例函数的主要性质解决问题

17．如图，在矩形ABCD中，AB=6，BC=8，⊙O是以BC为直径的圆，点P在AD边上运动(不运动至AD的两端)，BP交⊙O于Q，连结CQ。试解答下列问题：

① 设线段BP的长为x，CQ的长为y，求y关于x的函数关系式和自变量x的取值范围；

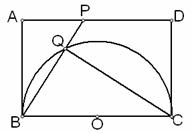
② 求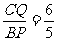时，△BQC与△PAB的面积比和AP的长。

16．点P为函数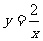的图象上一点，且点P到原点的距离为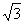，符合条件的点P的个数为(　 )

A　 0个　 B　 2个　 C　 4个　 D无数个

15．一次函数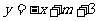，反比例函数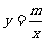，A为它们在第二象限的交点，S_△ABC=1，A点的坐标　　　　　　 。

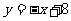设直线和双曲线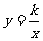(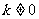)的交点为A、B。

求1)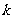为何值时，∠AOB＜90°；

2)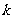为何值时，∠AOB＞90°

14．反比例函数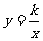的图象过点P(a,b)，其中a,b是方程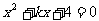的两个根，P点的坐标为　　　　 。

13．如图，A、C是函数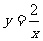的图象上关于原点O对称的任意两点，过A、B向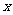轴引垂线，垂足分别为D、B，则四边形ABCD的面积为　　　　 。