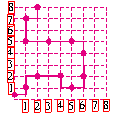
2.　　 如图为一辆公交车的得驶路线示意图，“●”表示停靠点，现在请你帮助小明完成对该公交车行驶的路线描述：起点站→(1，1)→…→终点站.　 　

　答案 　 1.解：如图： 　　 　 2.解：如图： 　　 　 3.解：起点站→(1，1)→(2，2)→(4，2)→(5，1)→(6，2)→(6，4)→(5，5)→(3，5)→(1，5)→(1，7)→(2，8).

综合训练题

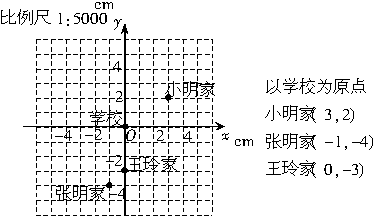
2.小明家在学校以东150m，再向北100m处，张明同学家在学校以西50m，再往南200m处，王玲同学家在学校以南150m处，建立适当的直角坐标系，在直角坐标系中画出这三位同学家的位置，并用坐标表示出来.

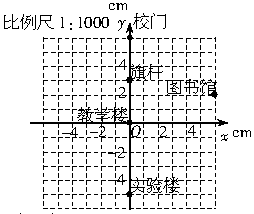
1.某学校校门在北侧，进校门向南走30米是旗杆，再向南走30米是教学楼，从教学楼向东走60米，再向北走20米是图书馆，从教学楼向南走60米，再向北走10 米是实验楼，请你选择适当的比例尺，画出该校的校园平面图.

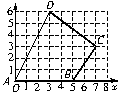
1.　　 如图所示的直角坐标系中，四边形ABCD各顶点坐标分别为A(0，0)，B(5，0)，C(7，3)，D(3，6)，你能求出这个四边形的面积吗？ 　 　2.已知长方形OABC在平面直角坐标系中的位置如图所示，点B的坐标为(3，-2)，则长方形的面积是多少？ 　

答案 　1.解：如图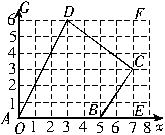： 　　 　　 S_{四边形ABCD} ＝ S_{四边形AEFG} － S_三角形ADG － S_三角形BCE － S_三角形CDF ＝ 7×6－×6×3－×(7-5)×3－×(7-3)×(6-3) 　　　　　　　　　　　　　＝ 42-9-3-6 　　　　　　　　　　　　　＝ 24.　 　2.解：因为点B的坐标为(3，-2)，所以AB＝|-2|＝2，BC=3. 　所以长方形的面积为2×3＝6.

强化训练题

[例7]在纸上建立直角坐标系，根据点的坐标描出下列各点：(0，0)，(5，3)，(3，0)，(5，1)，(5，-1)，(4，-2)，然后按照(0，0)→(5，3)→(3，0)→(5，1)→(5，-1)→(3，0)→(4，-2)→(0，0)的顺序用线段连结起来. 　　 (1)看看你得到的图案像什么？ 　　 (2)如果把这些点的横坐标都加上1，纵坐标都减去2.再按照原来的顺序将得到的各点用线段连结起来，这个图案与原图案在大小、形状、位置上有什么变化？ 　 [思考与解](1)建立平面直角坐标系，将各点描出，连结后我们可以得到一条可爱的小鱼，如图1. 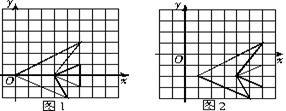　　 　　 (2)如果把这些点的横坐标都加上1，纵坐标都减去2，再按原来的顺序连结，仍得到一条小鱼，这条小鱼的大小、形状与原来的完全一样，它的位置可以看作将原来的小鱼向右平移1个单位长度，然后再向下平移两个单位长度得到，如图2.

[例8]如果将点P绕定点M旋转180°后与点Q重合，那么称点P与点Q关于点M对称，定点M叫做对称中心.此时，M是线段PQ的中点. 　 如图，在直角坐标系中，△ABO的顶点A、B、O的坐标分别为(1，0)、(0，1)、(0，0).点列P₁、P₂、P₃…中的相邻两点都关于△ABO的一个顶点对称：点P₁与点P₂关于点A对称，点P₂与点P₃关于点B对称，点P₃与P₄关于点O对称，点P₄与点P₅关于点A对称，点P₅与点P₆关于点B对称，点P₆与点P₇关于点O对称，….对称中心分别是A、B、O、A、B、O，…，且这些对称中心依次循环.已知点P₁的坐标是(1，1)，试求出点P₂、P₇、P₁₀₀的坐标. 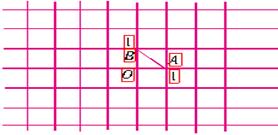　 　 [思考与解]根据所给的坐标可以知道O为坐标原点.由于点P₁与点P₂关于点A对称，且P₁的坐标是(1，1)，所以P₂的坐标是(1，-1)；点P₂与点P₃关于点B对称，所以P₃的坐标是(-1，3)；点P₃与P₄关于点O对称，所以P₄的坐标是(1，-3)；点P₄与点P₅关于点A对称，所以P₅的坐标是(1，3)；点P₅与点P₆关于点B对称，所以P₆的坐标是(-1，-1)；点P₆与点P₇关于点O对称，所以P₇的坐标是(1，1)，这样的话P₇与P₁重合.依次类推，反复循环，可以知道P₈与P₂重合、P₉与P₃重合、P₁₀与P₄重合、P₁₁与P₅重合、P₁₂与P₆重合、P₁₃与P₇重合(即与P₁重合)，由此推断，点Pn是以6为一个周期进行循环的.因此100除以6商是16余数为4，因此P_n的坐标与P₆的坐标相等为(1，-3).答案为P₂(1，-1)， P₇(1,1)，P₁₀₀(1，-3). [小结] 通过以上分析，在平面直角坐标系中，与点的坐标有关的探索问题中点的变化都是有周期性变化的.希望同学们认真探索、总结，以便做到熟能生巧.

第四节、竞赛数学

[例1]如果点M(1-x，1-y)在第二象限，那么点N(1－x，y-1)关于原点的对称点P在第几象限？ [分析]若抓住对称点的坐标特性这一解题关键，则可由点M(1-x,1-y)与点N(1－x,y-1)的横坐标相等、纵坐标互为相反数，知两点关于x轴对称，从而可确定出点N在第三象限.于是，点N关于原点的对称点P在第一象限. 　 解法一：∵点M(1-x，1-y)在第二象限， 　 ∴1-x＜0，1-y＞0. 　 ∴y-1＜0，则点N(1－x，y-1)在第三象限. 　 ∵点P与点N关于原点对称， 　 ∴点P在第一象限. 　 解法二：∵点M(1-x，1-y)与点N(1－x，y-1)关于x轴对称，且点M在第二象限， 　 ∴点N在第三象限. 　 ∵点P与点N关于原点对称， 　 ∴点P在第一象限. 　[小结](1)若不能根据题设条件获得1－x与y-1的正、负情况，就没有解法一； 　 (2)若不能发现点M与点N之间的对称关系，就没有解法二. 　 (3)有序实数对与坐标上的点一一对应，这就使得数与形结合起来.解题时可根据条件，运用数形结合的思想灵活解题.

[例2]国际象棋、中国象棋和围棋号称世界三大棋种.国际象棋中的“皇后”的威力可比中国象棋中的“车”大得多；“皇后”不仅能控制她所在的行与列中的每一个小方格，而且还能控制“斜”方向的两条直线上的每一个小方格.如图甲是一个4×4的小方格棋盘，图中的“皇后Q”能控制图中虚线所经过的每一个小方格. 　 在如图乙的小方格棋盘中有一“皇后Q”，她所在的位置可用“(2，3)”来表示，请说明“皇后Q”所在的位置“(2，3)”的意义，并用这种表示法分别写出棋盘中不能被该“皇后Q”所控制的四个位置. 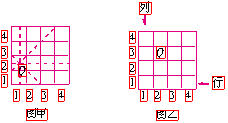　 　 [分析与解] 注意行与列的区别，点(2，3)的意义是第3行、第2列.故“皇后Q”可控制整个第3行和第2列，还可以控制(1，4)，(3，2)，(4，1)和(1，2)，(3，4).不能被该“皇后Q”所控制的四个位置是(1，1)，(3，1)，(4，2)，(4，4).

[例3]如图．围棋盘的左下角呈现的是一局围棋比赛中的几手棋．为记录棋谱方便，横线用数字表示．纵线用英文字母表示，这样，黑棋①的位置可记为(C，4)，白棋②的位置可记为(E，3)，则白棋⑨的位置应记为________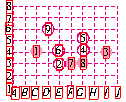． 　 　 [思考与解]本题平面直角坐标系中的横坐标用英文字母表示，根据坐标点位置的意义，易知白棋⑨的位置应记为(D，6)． 　 [例4]五子连珠棋和象棋、围棋一样，深受广大棋友的喜爱，其规则是：15×15的正方形棋盘中，由黑方先行，轮流弈子，在任一方向上连成五子者为胜．如图是两个五子棋爱好者甲和乙的对弈图；(甲执黑子先行，乙执白子后走)， 　 观察棋盘思考：若A点的位置记做(8，4)，甲必须在哪个位置上落子，才不会让乙在短时间内获胜？为什么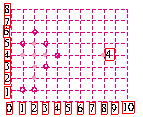？ 　 　 [思考与分析]由对弈规则可知：只有当任一方向(包括直线和斜线)上有五个子连在一起时才能获胜，观察棋盘，不难发现，甲必须首先截断乙方的(2，6)，(3，5)和(4，4)三颗白子，故必须在(1，7)或(5，3)处落子，方可不败． 　 解：甲必须在(1，7)或(5，3)处落子，因为若甲不首先截断以上两处之一，而让乙在(1，7)或(5，3)处落子，则不论截断何处，乙总有一处落子可连成五子，乙必胜无疑．

第五节、本章训练

基础训练题

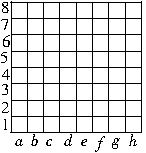
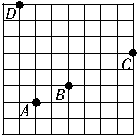
1.如图，将平行四边形ABCD向右平移2个单位长度，可以得到平行四边形A′B′C′D′，再将平行四边形A′B′C′D′向上平移2个单位长度，可以得到平行四边形A″B″C″D″，画出平移后的图形，并写出平行四边形A″B″C″D″各个顶点的坐标. 　　 　　 2.在如图所示的国际象棋棋盘中，双方四只马的位置分别是A(b，3)，B(d，5)，C(f，7)，D(h，2)，请在图中描出它们的位置. 　　　　 　　 3.如图是一个8×8的球桌，小明用A球撞击B球，到C处反弹，再撞击桌边D处.请选择适当的坐标系，并用坐标表示各点的位置. 　　　　

答案 　　 1.解：如图，A″(1，0)，B″(5，0)，C″(6，3)，D″(2，3). 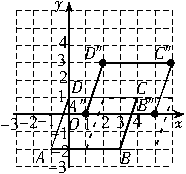　　 　　 2.解：如图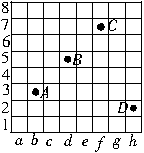： 　　　 　　 3.解：以A为坐标原点，则B(2，1)，C(6，3)，D(-1，6).

提高训练题

第二节、错解剖析

[例1]小虎正确地描出了各点，把它们连接起来，涂上阴影，如图所示. 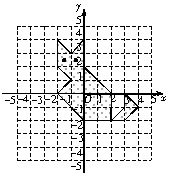　 　 小虎兴奋地说：“真没想到，分布在四个象限内的这些点，居然能连成一只可爱的小猫.” 　 不料，此话一出，又遭到小新的反对：“你说的话有毛病，坐标系内的点并不是都分布在四个象限中，还有些点在坐标轴上，它们不属于任何一个象限.比如，本题中(-2，0)，(2，0)，(3，0)三个点在横轴上，(0，-2)，(0，2)，(0，4)三个点在纵轴上”. 　 小虎马上更正：“我说错了，我忘了在坐标轴上的点不属于任何象限，就像在横轴上的点都不能在纵轴一样.” 　 没想到，小新又纠正道：“这话也有问题，原点是一个特殊的点，它既在横轴上，也在纵轴上.” 　 这时，老师又问了小虎一个问题：“你能根据这只猫眼睛的大致位置，说出它们的坐标分别是什么吗？” 　 小虎思考了一下，答道：“它两只眼睛的坐标分别是(-1.5，2.5)和(-0.5，2.5).” 　 老师肯定了他的回答，又布置了一道思考题： 　 请在坐标系中，描出到横轴距离为4、到纵轴距离为5的点. 　 小虎一听，不假思索地说：“这有什么难的，不就是描出坐标为(4，5)的点吗？”他边说边在图中画出点M，没等画完就发现自己错了，急忙更正：“哦--错了！到横距离为4，不是说横坐标为4；到纵轴距离为5，也不是说纵坐标为5.所以，这个点的坐标不是(4，5)，而应该是(5，4)，这个点N才符合条件--这次，总该没错了吧.” 　 小新一听，说：“你考虑得不全面，还有三个点呢.你看，点P(5，-4)，Q(-5，-4)和R(-5，4)三个点是不是也符合条件，别忘了距离是非负数，一个点到横轴的距离是它的纵坐标的绝对值，到纵轴的距离是它的横坐标的绝对值.”

第三节、思维点拨

18.附加题：(20分)

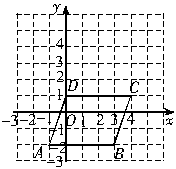
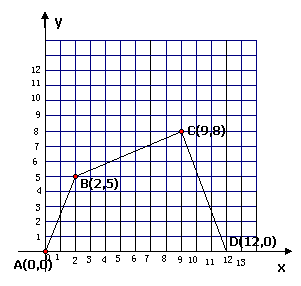　　 在如图所示的直角坐标系中，四边形ABCD的各个顶点的坐标分别是A(0，0)，B(2，5)，C(9，8)D(12，0)确定这个四边形的面积。你是怎样做的？

16．(10分)如图：左右两幅图案关于轴对称，左图案中左右眼睛的坐标分别是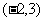，，嘴角左右端点的坐标分别是 ，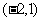

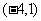
⑴试确定右图案的左右眼睛和嘴角左右端点的坐标

⑵你是怎样得到的？与同伴交流。

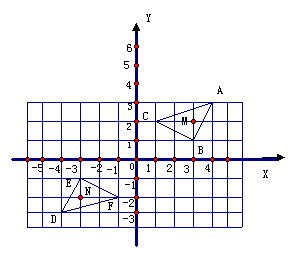　17．(10分)如图：三角形DEF是三角形ABC经过某种变换后得到的图形，分别写出A与点D，点B与点E，点C与点F的坐标，并观察它们的关系，如果三角形ABC中任一点M的坐标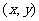，那么它的对应点N的坐标是什么？

15．建立适当的直角坐标系，表示边长为3的正方形各顶点的坐标。(8分)

14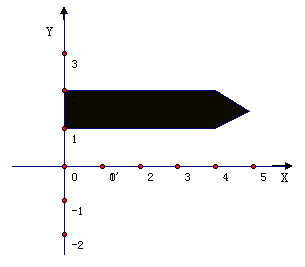．如图：铅笔图案的五个顶点的坐标分别是(0，1) (4，1)　 (5，1.5)

(4，2) (0，2)将图案向下平移2个单位长度，作出相应图案，并写出平移后相应5点的坐标。(10分)