练习册

  • 练习册
  • 试题
     0  209548  209556  209562  209566  209572  209574  209578  209584  209586  209592  209598  209602  209604  209608  209614  209616  209622  209626  209628  209632  209634  209638  209640  209642  209643  209644  209646  209647  209648  209650  209652  209656  209658  209662  209664  209668  209674  209676  209682  209686  209688  209692  209698  209704  209706  209712  209716  209718  209724  209728  209734  209742  447090 

    3．填写数学活动评价表．如果有可能的话，教师应建议学生写一篇调查的小论文．

    试题详情

    2．依数学活动步骤展开活动．

    试题详情

    1．先组织全班讨论，然后3人组成一个活动小组进行活动．

    试题详情

    3．在经历克服困难并获得成功的过程中，增进应用数学的自信心，积累数学活动的经验，培养并发展良好的合作意识和能力．

    [活动过程]

    试题详情

    2．扩大学生的思维视角，深化学生对知识的理解，培养学生主动应用数学的意识和综合运用所学知识解决问题的能力．

    试题详情

    1．经历数据的收集、整理、描述和分析的过程；能根据数据处理的结果，做出合理的判断和预测，并在这一过程中体会统计对决策的作用。

    试题详情

    活动过程
    		 师生行为
    		 设计意图
    活动1：报告位置
    1.1 创设情境：游玩中，小明、小华走散了，他俩赶紧用电话向老师报告位置，小明说：“老师，我们这里坐标为(200，200)”，小华说：“不对，我们这里坐标为(0，300)。
    想一想：①他们在同一个位置，为什么坐标不同呢？(实际上他们说的坐标都对。)
    ②老师知道他们在哪个景点吗？为什么？
    1.2 探究：若小明小华都在温峡水库，应该怎样报告自己的位置老师才明白？
    　1.3　 应用：请每一位同学选择一个游玩的景点，然后同座位的同学用坐标相互报告自己的位置，看对方能否准确找到？
    		 　
    学生动手操作、参与讨论、发表见解。
    　
    教师引导学生反思、总结，教师本活动中应重点关注：
    ①学生在活动中，发表个人见解的勇气；②学生能否寻找到解决问题的方法。
    　
    　
    		 　
    通过给学生提供现实背景，吸引学生的注意力，激发学生探究欲望。
    在应用活动中通过同学之间互相帮助、互相评价，培养学生合作意识与交流能力，使学生掌握用坐标向别人告诉自己位置的方法。
    活动2：室内寻宝
    2.1 创设情境：已知第一排甲同学已知第一排甲同学坐标为(－2，3)，乙同学坐标为(2，3)，藏宝地点的坐标为(－3，－1)，你知道宝物藏在哪位同学的座位下吗？
    2.2 探究：如何建立平面直角坐标系。
    2.3 应用：请每个同学记下自己的坐标，老师让坐标出现在屏幕上的同学举起手，拿起花束，其它同学观察所组成的图案。
    　
    		 　
    学生观察、思考、交流，发表个人见解，老师深入学生，倾听学生交流，适时点拨。
    　 教师应重点关注：
    　 ①学生是否能发现甲、乙两同学的坐标特点；
    ②学生能否主动与同学合作、交流各自想法。
    		 　
    通过游戏调动学生进一步参与活动和学习数学的积极性，在合作中学会尊重和理解他人的见解。在寻找坐标系的过程中，培养学生观察能力、交流能力以及综合运用所学知识解决问题的能力，使学生进一步体会坐标系这个模型在确定物体位置中的作用。
    活动3：电话传图
    3.1创设情境: 小菲非常关心北京2008年奥运，特为奥运会设计一个船的图案“　　 ”，正准备给北京方面发个传真，不巧，停电了，怎么办？小菲灵机一动，在图上比比画画一翻，很快用电话将图案准确无误地传到北京，你知道小菲用得是什么办法吗？
    3.2 探究：传递的办法。
    3.3 应用：请设计一个简单而有趣的图案(老师可提供参考图案，学生可采用)，按照刚才方法奇数排和偶数排的同学相互传递，看看他人能否收到你的图形。
    		 　
    学生讨论交流，动手操作、思考。
    教师应重点关注：
    ①学生把实际问题抽象成数学问题的能力；
    ②运用所学知识与方法创造性解决问题的能力；
    ③学生动手的能力；
    ④学生在设计的图案中所体现的情感态度和价值观。
    　
    		 ①让学生经历问题情境--建立数学模型--进而解决问题的过程，培养学生创造性用坐标法解决问题的能力，从而发展学生的应用意识。②让学生初步的感受到坐标系是勾通图形与数量之间关系的桥梁，渗透数形结合的思想，渗透事物之间相互联系、相互转化的辩证唯物主义观点。③
    给学生提供一个自我展示，自我表现的机会，从而增强学生学好数学的信心。
    　
    小结：
    问题：
    在实际问题中遇到什么情况时，可用坐标法解决？怎样用坐标法解决？你能再举一些用坐标法解决的实例吗？
    作业布置：
    收集一些校园或自己家附近有代表性的建筑，绘制出相关的平面分布图。
    		 　
    学生着重对活动过程中的体验、感受、认识、收获进行回顾与反思。
    教师对学生进步给予充分的肯定，树立学生学好数学的自信心。
    　
    		 　
    通过回顾与反思，使学生进一步体会坐标法在日常生活中的广泛应用，获得一些研究问题方法与经验。

    试题详情

    活动流程图
    		 活动内容和目的
    活动1：报告位置
    		 学生用坐标向老师报告在游玩的景点位置，使学生感受坐标系的作用。
    活动2：室内寻宝
    		 已知教室第一排甲、乙两同学和藏宝地点坐标，请寻找宝物位置，通过坐标系的寻找，培养学生综合运用所学知识解决问题的能力。
    活动3：电话传图
    		 探究怎样用电话将一个船的图案传送给远方的朋友？通过探索传递的办法，培养学生创造性运用所学知识解决问题的能力，发展学生应用意识。

    试题详情

    教
    学
    目
    标
    		 知识与技能
    		 巩固由坐标描点、由点写坐标的技能，掌握用坐标表示物体位置的方法。
    过程与方法
    		 经历“问题情境-建立坐标系模型-解释与应用”的过程，体验数是描述现实世界的重要手段，提高分析问题、解决问题的能力。
    情感与态度
    		 感受数学在日常生活中的广泛应用，体会与他人合作交流的重要性。
    重点
    		 能应用坐标法解决实际问题，培养学生的应用意识。
    难点
    		 把实际问题转化为数学问题，并能根据实际情况建立适当的坐标系

    试题详情

    答案 　 一、1. (-1，5)　　 2. (-1，2)　　 3. 0 　　　　　4. 第二　　　　　　　 5. (3，4) 　 二、6.A　　　 7.B　　　 8.B　　　 9.B　　　 10.B 　 三、11. [解题思路]　(1) 在平面上确定点的位置至少需要两个数据. 　　(2) 车到第五大道3路去的路线很多，可先列出几条较近的再择优选取. 　　 解： (1) 只用“道”或“路”一个数，不能确定点的位置. 　　　　　　　 (2) 要使路程最短，共有五种方法. 　　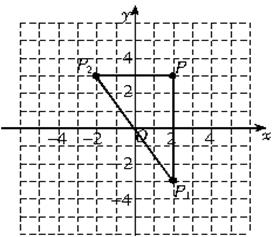① (1，2)→(2，2)→(3，2)→(4，2)→(5，2)→(5，3) 　　 ② (1，2)→(2，2)→(3，2)→(4，2)→(4，3)→(5，3) 　　 ③ (1，2)→(2，2)→(3，2)→(3，3)→(4，3)→(5，3) 　　 ④ (1，2)→(2，2)→(2，3)→(3，3)→(4，3)→(5，3) 　　 ⑤ (1，2)→(1，3)→(2，3)→(3，3)→(4，3)→(5，3) 　　 12.[解题思路]我们可以看到，本题分三问，每一问都是下一问的基础，因此我们不能因为前边的问题简单而麻痹大意，因为一步错，步步错.所以我们必须认真对待，一丝不苟的完成 　　 解：(1)如图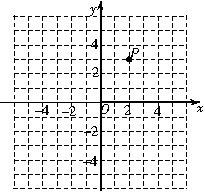： 　　 　　 (2)P1(2，-3)，P2(-2，3). 　　 (3)如图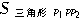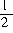：=PP1×PP2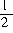＝×6×4＝12. 　　

    试题详情


    同步练习册答案