
2.如果“两角及一边”条件中的边是其中一角的对边。
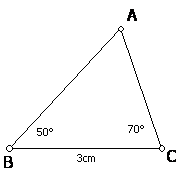
例如下图,在△ABC中,∠A=60°,∠B=50°,BC=3cm,你能画出一个三角形,使它的两个内角分别是60°和50°,而且60°所对的边为3cm吗?你画的三角形与△ABC全等吗?
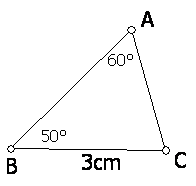
(提示:这里的条件与1中的条件有什么相同点与不同点?你能将它转化为1中的条件吗?)
议一议:
改变△ABC中相应的角度和边长,你能得到同样的结论吗?
于是我们又得到两个判定两个三角形全等的方法:
两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。
两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”。
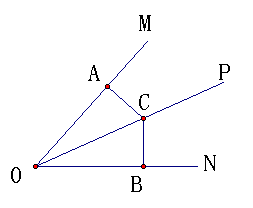
例题1:如图,OP是∠MON的角平分线,C是OP上一点,CA⊥OM,CB⊥ON,垂足分别为A、B,△AOC≌△BOC吗?为什么?
练习:第142页第1、2、3题
议一议:(略)
小结:
本节课我们又学习了判定两个三角形全等的两种方法“角边角”和“角角边”,这样连“边角边”我们一共学习了三种判定两个三角形全等的方法了。同学们在应用这些方法解决问题时,要具体问题具体分析,找出正确的途径。
教学素材:
A组题:
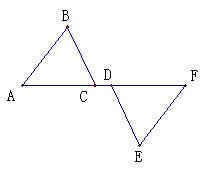
1.如图,B点是线段EF的中点,BA=BC,AE=CF。△ABE和△CBF全等吗?说说你的理由。

如图5-5-4,AB=DF,AC=DE,BE=CF。你能找到一对全等三角形吗?说明你的理由。

B组题:
你还记得怎样用尺规作一个角等于已知角吗?你能说明其中的道理吗?
小明回顾了作图的过程,并进行了如下的思考:


OC=O C
C ,OD=O
,OD=O D
D ,CD=C
,CD=C D
D
△OCD≌△O C
C D
D
∠DOC=∠D O
O C
C
你能说明每一步的理由吗?
2.如图,已知∠ACB=∠BD=90°,若要使△ACB≌△BDA,还需要什么条件?把它们分别写出来。
错误!不能识别的开关参数。错误!不能识别的开关参数。
B组题:
例:已知:如图,在△ABC和△A′B′C′中,CD、C′D′分别是高,并且AC=A′C′,CD=C′D′,∠ACB=∠A′C′B′。
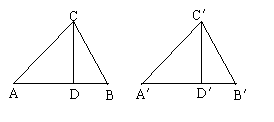 求证:△ABC≌△A′B′C′
求证:△ABC≌△A′B′C′
 例题1:书第145页
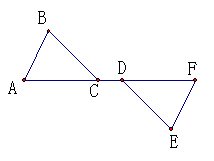
例题1:书第145页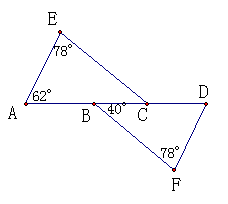 如图,点A、B、C、D在同一条直线上,AB=CD,△EAC和△FDB全等吗?为什么?
如图,点A、B、C、D在同一条直线上,AB=CD,△EAC和△FDB全等吗?为什么?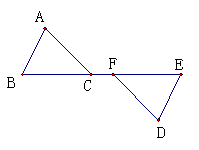 若△ABC和△DEF全等,则还可以进一步得到哪些结论?
若△ABC和△DEF全等,则还可以进一步得到哪些结论?
练习:第146页第2、3题
小结:
到本节课为止,我们一共学习了四种判定两个三角形全等的方法,“边边边”,“角边角”,“角角边”,“边角边”。同学们既要知道每一个方法的内容,又要学会用这些方法去判定两个三角形全等,解决实际问题。
教学素材:
A组题:
1.已知:如图,△ABC中,AB=AC,AD是高,则______≌______。依据是______,BD=______,∠BAD=______.
3.熟练使用“分析综合法”探求解题思路。
教学素材:
A组题:
2.使用“HL”公理时,必须先得出两个直角三角形,然后证明斜边和一直角边对应相等。
2、填空:
(1) 如图,已知AO=DO,∠AOB与∠DOC是对顶角,还需补充条件___________=_____________,就可根据“SAS”说明△AOB≌△DOC;
(2)

B组题:
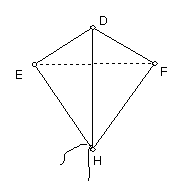
小明做了如图所示的风筝,其中∠EDH=∠FDH,ED=FD,将上述条件标注在图中,小明不用测量就能知道EH=FH。你知道为什么吗?


(2)试用一条直线将所给的长方形分成两个全等三角形,有多少种分法?你发现了什么结论?

B组题:
1、分别找出各题中的全等三角形,并说明理由。



|
2.填空
如图,已知AO=DO,∠AOB与∠DOC是对顶角,还需补充条件______________=_______________,就可根据“ASA”说明△AOB≌△DOC;或者补充条件_______________=_______________,就可根据“AAS”,说明△AOB≌△DOC。(若把“AO=DO”去掉,答案又会有怎样的变化呢?)

B组题:
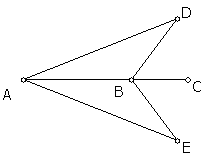 如图,一艘轮船沿AC方向航行,已知轮船在A点测得航线两侧的灯塔与航线的夹角相等,当轮船到达B点时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等,为什么?
如图,一艘轮船沿AC方向航行,已知轮船在A点测得航线两侧的灯塔与航线的夹角相等,当轮船到达B点时测得这两个灯塔与航线的夹角仍然相等,这时轮船与两个灯塔的距离是否相等,为什么?

新课讲解:
同学们会说这需要量一下这个三角形的边长和内角的度数,那么请问:你准备量哪几条边长,哪几个内角的度数?能尽量少吗?
我们一起来分析:
只知道一个条件(一条边或一个角)画三角形,能保证画出的三角形与△ABC全等吗?
知道两个条件画三角形,有几种可能的情况?(两条边或两个角或一条边和一个角)
每种情况下作出的三角形一定与△ABC全等吗?我们来试一次。
量得△ABC中,BC=3cm,∠B=50°,画画看。
还是不行,当然如果我们只知道△ABC中其它两个条件,例如只知道两个角的度数,也还是不能保证作出的三角形与△ABC全等。有兴趣的话可以课后试试。
如果知道三个条件画三角形,你能说出有哪几种可能的情况?
(有四种可能:三条边、三个角、两边一角和两角一边)
做一做:
在△ABC中,已知∠A=70°,∠B=50°,∠C=60°,你能画出一个与△ABC全等的三角形吗?
(不能,因此三个内角对应相等的两个三角形不一定全等)
在△ABC中,已知AB=2.8cm,∠A=70°,AC=2.5cm,你能画出一个与△ABC全等的三角形吗?
 两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”。
两边和它们的夹角对应相等的两个三角形全等,简写成“边角边”或“SAS”。
例题1:例1:如图,AB=AD,
∠BAC=∠DAC,请问:△ABC
和 △ADC是否全等?为什么?
练习:第139页第1、2题
小结:本节课我们通过操作实践,发现了判定两个三角形全等的第一个方法--边角边。在解决实际问题时,特别在说明两个三角形全等的理由时,应根据已知条件及图形中的有关条件,依照“SAS”加以说明。
教学素材:
A组题:
1.分别找出各题中的全等三角形,并说明理由。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com