
(二)加强反比例函数与正比例函数的对比
在复习“第11章 一次函数”内容的基础上,引进本章内容。应该有意识地加强反比例函数  (k为常数,
(k为常数, )与正比例函数
)与正比例函数 (k为常数,
(k为常数, )之间的对比,对比可以从如下几方面进行:
)之间的对比,对比可以从如下几方面进行:
1.两种函数的解析式有何相同与不同?两种函数的图象的特征有何区别?
2.在常数 相同的情况下,当自变量 变化时两种函数的函数值 的变化趋势有什么区别?
3.两种函数中 的取值范围有何不同?常数 的符号改变对两种函数图象所处象限的影响如何?
回答是这样的:
1.两种函数的解析式的相同点是,自变量只有一个,即x,都有一个常数k,且 ;不同点是自变量 在解析式中的位置不同,正比例函数的解析式 的右边是一个整式,不为0的常数k是自变量x的系数,而反比例函数的解析式
;不同点是自变量 在解析式中的位置不同,正比例函数的解析式 的右边是一个整式,不为0的常数k是自变量x的系数,而反比例函数的解析式 的右边是一个分式,自变量x处在分母的位置,不为0的常数k处在分子的位置。
的右边是一个分式,自变量x处在分母的位置,不为0的常数k处在分子的位置。
两种函数的图象都分布在两个象限内,这是相同之处;不同点在于正比例函数的图象是一条直线,而反比例函数的图象是两支曲线。正比例函数的图象经过原点,而反比例函数的图象不经过原点。
2.在常数 相同的情况下,当自变量x增大(减小)时,正比例函数的y值增大(减小),而反比例函数的y值减小(增大);在常数
相同的情况下,当自变量x增大(减小)时,正比例函数的y值增大(减小),而反比例函数的y值减小(增大);在常数 相同的情况下,当自变量x增大(减小)时,正比例函数的y减小(增大),而反比例函数的 t值增大(减小)。
相同的情况下,当自变量x增大(减小)时,正比例函数的y减小(增大),而反比例函数的 t值增大(减小)。
3.当常数 的符号改变时,两类函数图象所处的象限都会随之改变。当 时,两类函数的图象都分布在一、三象限;当
时,两类函数的图象都分布在一、三象限;当 时,两类函数的图象都分布在二、四象限。
时,两类函数的图象都分布在二、四象限。
对于这些问题,不要急于给出答案,应该注意鼓励学生积极探究,在这样的氛围中,学生的数学思维和兴趣会被激发起来,对所学内容的掌握也就更牢固。
(一)注意做好与已学内容的衔接
教科书在“第11章 一次函数”已经给出了函数的一般概念以及自变量、函数值等概念.,学生对函数已经形成了初步的认识。反比例函数的教学,一方面要以前面所学的函数概念及相关知识为基础,另一方面可以反过来进一步深化对函数内涵的理解和掌握。
从学生第一次接触函数所蕴涵的“变化与对应”思想至今已经半年有余,学生对与函数相关的概念不可避免会有所遗忘或生疏。因此,学习好本章的关键是处理好新旧知识的联系,尽可能地减少学生接受新知识的困难。例如,在引进反比例函数概念时,要适时复习第11章中的函数、自变量、函数值、正比例函数、一次函数等定义或概念,为反比例函数的学习做好铺垫。这样,学生就能够比较顺利地接受和掌握反比例函数的概念和性质。
(二)注重数学思想的渗透
从数学自身的发展过程看,正是由于变量与函数概念的引入,标志着初等数学向高等数学迈进,尽管本章讲述的反比例函数仅是一种最基本、最初步的函数,但其中蕴涵的数学思想和方法,对学生观察问题、研究问题和解决问题都是十分有益的。
我们知道函数的定义不是惟一的,从不同的理解角度出发可以给出函数不同的定义。教科书在“第11章 一次函数”已经给出了函数定义,这个定义突出了数学中的变化与对应的数学思想,其内涵主要有两个:首先,两个变量互相联系,一个变量变化时另一个变量也发生变化;其次,函数与自变量之间是单值对应关系,自变量的值确定后,函数的值是唯一确定的。
在本章的编写时,一方面十分注意具体题目的分析及求解过程,另一方面更加注重一些重要的数学思想,如变化与对应的数学思想、数形结合的思想以及转化思想的传授和渗透。
(三)课程学习目标
本章内容的设计与编写以下列目标为出发点:
1.使学生理解并掌握反比例函数的概念,能根据实际问题中的条件确定反比例函数的解析式 ,能判断一个给定函数是否为反比例函数;
,能判断一个给定函数是否为反比例函数;
2.能描点画出反比例函数的图象,会用代定系数法求反比例函数的解析式,进一步理解函数的三种表示方法,即列表法、解析式法和图象法的各自特点;
3.能根据图象数形结合地分析并掌握反比例函数 的函数关系和性质,能利用这些函数性质分析和解决一些简单的实际问题;
的函数关系和性质,能利用这些函数性质分析和解决一些简单的实际问题;
4.探索现实生活中数量间的反比例关系,在解决实际问题的过程中,进一步体会和认识反比例函数这种刻画现实世界中特定数量关系的数学模型;
5.使学生在学习一次函数之后,进一步理解常量与变量的辨证关系和反映在函数概念中的运动变化观点,进一步认识数形结合的思想方法。
(一)本章知识结构框图

18. 如图,长方形ABCD是一块釉面砖,居室装修时需要在此砖上截取一块呈梯形
如图,长方形ABCD是一块釉面砖,居室装修时需要在此砖上截取一块呈梯形
状的釉面砖APCD.
(1)请在AB边上找一点P,使∠APC=120°;
(2)试着叙述选取点P的方法及其选取点P的理由.
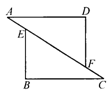
17.如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,下面有4个判断:
(1)AD=CB;(2)AE=FC;(3)∠B=∠D;(4)AD∥BC.
请用其中3个作为已知条件,余下1个作为结论,编一道数学问题,并写出解答过程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com