
平移前后的坐标变化及点的坐标特征、应用
点的表示及描点方法、点的特征、平移的应用。
理解和掌握坐标系有关概念,体会图形的变换,学会运用平移变换规律进行作图描点,培养合作交流、数形结合的思想,体会坐标系的实际应用价值。
5、 某气球内充满的一定质量的气体,当温度的不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如下图所示。当气球内气体的气压大于140 kPa时,气球将爆炸,为了安全起见,气体体积应( )
某气球内充满的一定质量的气体,当温度的不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如下图所示。当气球内气体的气压大于140 kPa时,气球将爆炸,为了安全起见,气体体积应( )
A、不大于 m2
B、不小于
m2
B、不小于 m2
m2
C、不大于 m2 D、不小于
m2 D、不小于 m2
m2
解:因为当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数。
设 
因为函数图象过A(0.8,120)。代入 中得
中得
所以
即 。
。
∵96>0,所以p随V的增大而减小,当p=140kPa时, 。所以为了安全起见,气球内的气压应不大于140kPa,气体的体积应不小于
。所以为了安全起见,气球内的气压应不大于140kPa,气体的体积应不小于 。
。


|
板书设计:
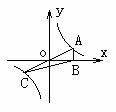
4、(1)若点(x1,y1),(x2,y2),(x3,y3),都在反比例函数的图象上,并且x1<0<x2<x3,则下列各式中正确的是( )
A、y1<y2<y3 B、y2<y3 < y1 C、y3< y2< y1 D、y1 <y3<y2
 (2)已知反比例函数
(2)已知反比例函数 的图象上有两点A(x1,y1),B(x2,y2),且x1<x2,则y1-y2的值是( )
的图象上有两点A(x1,y1),B(x2,y2),且x1<x2,则y1-y2的值是( )
A、正数 B、负数 C、非正数 D、不能确定
(3)正比例函数y=kx(k>0)与反比例函数 的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连接BC,若△ABC的面积为S,则( )
的图象相交于A、C两点,过A作x轴的垂线交x轴于B,连接BC,若△ABC的面积为S,则( )
A、S= 1 B、S= 2 C、S= 3 D、S的值不确定
点评:(1)因反比例函数的表达式具体,所以其图象具体,因 ,所以三点(
,所以三点( ),(
),( ),(
),( )的前后位置可确定于是可得
)的前后位置可确定于是可得 ,
, ,
,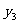 的关系,也可直接代入表达式内和实数大小比较方法判定;
的关系,也可直接代入表达式内和实数大小比较方法判定;
(2)由A、B两点的横坐标没有和O作比较,所以A、B两点的位置可分为两种 情况讨论;
(3)因△AOB的面积易求,要求△ACB的面积只需找到△APB和△BOC的关系,发现AO=CO,而且高相同,所以面积相等。
3、如下图,在同一直角坐标系中,正比例函数y=(m-1)x与反比例函数 的图象的大体位置不可能是(
)
的图象的大体位置不可能是(
)

解析:当m-1>0时,m>1时,4m>0,此时直线过一、三象限。双曲线位于第一、三象限,A可能,D不可能;
当m-1<0时,即m<1,分两种情况:0<m<1或m<0。当m<0时,直线过二、四象限,双曲线位于二、四象限;
当0<m<1时,直线过二、四象限,此时,4m>0,双曲线在第一、三象限,所以B、C都有可能,故不可能的是D。
点评:要判断直线和双曲线的位置关系,借助于它们的字母系数的符号,在这里,要判断m-1与4m的符号,进而选择合理答案,因不确定其符号,所以分两种情况进行讨论,当m-1>0时,4m>0,故A对,D不对;当m-1<0又有两种情况:0<m<1或m<0,而前者又4m>0,故B对,后者又4m<0,故C对。
做一做“
已知y=y1+y2,y1与x成反比例,y2与x2成正比例,并且x=2时,y=14;x=3时, ,求y与x之间的函数表达式。
,求y与x之间的函数表达式。
分析:依据正比例、反比例函数的定义,利用待定系数法求得其比例系数,从而求出y与x之间的函数关系式。
解:设 ,
, ,则
,则 ,将(2,14),(3,
,将(2,14),(3, )代入上式得
)代入上式得
 。 解得
。 解得 。
。
∴函数关系式为 。
。
点评:(1)一个反比例函数和一个正比例函数相加,构成一个新的函数,从形式上较为复杂,但是用待定系数法求系数的方法一样。
(2)要将 设成不同的参数。
设成不同的参数。
2、若反比例函数 ,当x>0,y随x的增大而增大,则一次函数y=kx-k的图象经过第几象限( )
,当x>0,y随x的增大而增大,则一次函数y=kx-k的图象经过第几象限( )
A、一、二、三 B、一、二、四 C、一、三、四 D、二、三、四
解:∵x>0时,y随x的增大而增大。
∴k<0,
∴一次函数y=kx-k的图象过一、二、四,故选B。
点评:要判断y=kx-k的位置,需知道k的符号,由已知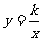 ,当x>0时,y随x的增大而增大,所以k<0。
,当x>0时,y随x的增大而增大,所以k<0。
问题1:你能举出现实生活中有关反比例函数的几个例子吗?
问题2:说一说函数 和
和 的图象的联系和区别。
的图象的联系和区别。
先由学生小组交流本单元的小结,再进行小组汇报,老师在旁适时指导,提问,鼓励。学生分小组合作交流,归纳本单元的知识体系,以及对每个知识块的认识,由上面两个问题作牵引,完成本单元的知识体系。
教师应重点关注:
①关注学生的复习过程,观察学生智力、情感的达标情况。
②对函数概念及图象、性质的理解。
③关注数学活动对学生发展的影响,学生能否从函数图象中敏锐地获取函数的相关信息,是否善于对实际问题进行分析,并灵活运用所学知识解决实际问题。
(四)突破知识的难点和重点
本章的重点是反比例函数的概念、图象和性质,图象是直观地描述和研究函数的重要工具。教材中给出了大量的具体的反比例函数的例子,用以加深学生对所学知识的理解和融会贯通。本章的难点是对反比例函数及其图象和性质的理解和掌握,教学时在这方面要投入更多的精力。
尽管本章中反比例函数的内容还是比较初级的知识,但是对这些知识的掌握却是为学习后续的函数知识打下基础。因此,教学中对本章基本知识和基本技能的要求不能有丝毫降低。要适时安排适当难度的习题,以使学生对基础知识形成深刻的印象、对基本技能达到熟练的程度。
有条件的地方应尽可能使用信息技术,在本章“信息技术应用”栏目中,给出了k变化时,反比例函数  (k为常数,
(k为常数, )的图象是如何变化的。尽管这一性质不是必修内容,但有兴趣和学有余力的同学却可以从中获益。
)的图象是如何变化的。尽管这一性质不是必修内容,但有兴趣和学有余力的同学却可以从中获益。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com