4．化简______．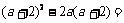

3．单项式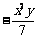的系数是______，次数是______．

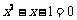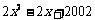2．已知：，则的值为______．

1．请你写出一个二次三项式：______．

(三)情感与价值观要求

　　 在探索提公因式法分解因式的过程中学会逆向思维，渗透化归的思想方法．

　　 教学重点:用提公因式法分解因式．

　　 教学难点:何确定公因式以及提出公因式后的另外一个因式．

　　 教学方法:导发现法．

　　 教学过程

　　 Ⅰ．提出问题，创设情境

　　 [师]请同学们完成下列计算，看谁算得又准又快．(出示投影片)

　　 (1)20×(-3)²+60×(-3)

　　 (2)101²-99²

　　 (3)57²+2×57×43+43²

　　 (学生在运算与交流中积累解题经验，复习乘法公式)

　　　 [师]在上述运算中，大家或将数字分解成两个数的乘积，或者逆用乘法公式使运算变得简单易行，类似地，在式的变形中，有时也需要将一个多项式写成几个整式的乘积形式，这就是我们从今天开始要探究的内容──因式分解．

　　 Ⅱ．导入新课

　　 1．分析讨论，探究新知．

　　 出示投影片

　　 把下列多项式写成整式的乘积的形式

　　 (1)x²+x=_________

　　 (2)x²-1=_________

　　 (3)am+bm+cm=__________

　　 [生]根据整式乘法和逆向思维原理，可以做如下计算：

　　 (1)x²+x=x(x+1)

　　 (2)x²-1=(x+1)(x-1)

　　 (3)am+bm+cm=m(a+b+c)

　　 [师]像这种把一个多项式化成几个整式的积的形式的变形叫做把这个多项式因式分解，也叫把这个多项式分解因式．

　　 可以看出因式分解是整式乘法的相反方向的变形，所以需要逆向思维．

　　 再观察上面的第(1)题和第(3)题，你能发现什么特点．

　　 [生]我发现(1)中各项都有一个公共的因式x，(2)中各项都有一个公共因式m，是不是可以叫这些公共因式为各自多项式的公因式呢？

　　　 因为ma+mb+mc=m(a+b+c)．

　 　于是就把ma+mb+mc分解成两个因式乘积的形式，其中一个因式是各项的公因式m，另一个因式a+b+c是ma+mb+mc除以m所得的商，像这种分解因式的方法叫做提公因式法．

　　 2．例题教学，运用新知．

　 　[例1]把8a³b²-12ab³c分解因式．

　 　[例2]把2a(b+c)-3(b+c)分解因式．

　 　[例3]把3x³-6xy+x分解因式．

　 　[例4]把-4a³+16a²-18a分解因式．

　　 [例5]把6(x-2)+x(2-x)分解因式．

　　 (让学生利用提公因式法的定义尝试独立完成，然后与同伴交流解题心得，教师深入到学生中去发现问题，并对有困难的学生进行适时的引导和启发，最后师生共同评析、总结)

　总结：有时多项式的各项从表面上看没有公因式，但将其中一些项变形后，但可以发现公因式，然后再提取公因式．

　　 Ⅲ．随堂练习

　　 1．课本P194练习1、2、3．

(二)能力训练要求

　　 1．使学生了解因式分解的概念，以及因式分解与整式乘法的关系．

　　 2．了解公因式概念和提取公因式的方法．

　　 3．会用提取公因式法分解因式．

(一)教学知识点

　　 1．因式公解、公因式．

　　 2．用提公因式法分解因式．

(一)这三个式子都是底数相同的幂相乘．