
5.(a-2b)2的结果是[ ]
A.a2-2ab+4b2 B.a2+4b2 C.a2-4b2 D.a2-4ab+4b2
4.下列各式可以用平方差公式的是[ ]
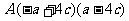
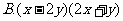
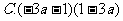
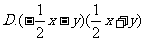
3.计算 (3x²y+9xy²)÷(6xy)的结果是[ ]
A.2x+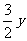 B.
B.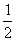 x+
x+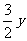 C.
C. 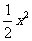 +
+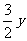 D.
D. 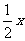 +
+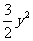
2.下列计算中,正确的是[ ]
A.a2+2a2=3a4 B.2x3·(-x2)=-2x5 C.(-2a2)3=-8a5 D.6x2m÷2xm=3x
1.有一道计算题:(-a4)2,李老师发现全班有以下四种解法,
①(-a4)2=(-a4)(-a4)=a4·a4=a8;
②(-a4)2=-a4×2=-a8;
③(-a4)2=(-a)4×2=(-a)8=a8;
④(-a4)2=(-1×a4)2=(-1)2·(a4)2=a8;
你认为其中完全正确的是[ ]
A.①②③④ B.①②④ C.②③④ D.①③④
28.图5-1是一个长为2 m、宽为2 n的长方形, 沿图中虚线用剪刀均分成四块小长方形, 然后按图5-2的形状拼成一个正方形.
 (1)、你认为图5-2中的阴影部分的正方形的边长等于多少?
(1)、你认为图5-2中的阴影部分的正方形的边长等于多少?
(2)、请用两种不同的方法求图5-1中阴影部分的面积.
方法1:
方法2:
(3)、观察图5-2你能写出下列三个
代数式之间的等量关系吗?
代数式: 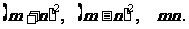
(4)、根据(3)题中的等量关系,解决如下问题:
若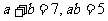 ,则
,则 =
.
=
.
答案及提示:
1-10 BCACA
DBDAB 11)-2x3y 12)3x 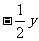 13) ±3
13) ±3
14) 2 15)12 16)550 17) n(n+2)+1=(n+1)2 18) m(m-2)2 19) 4 20)24
21)解:李老汉吃亏了.原来的种植面积为a2,变化的种植面积为(a+4)(a-4)=a2-16
因为a2> a2-16所以李老汉吃亏了.
22)第一处是(-a-b)3=-(a+b)3 第二处是2(a+b)3≠8(a+b)3
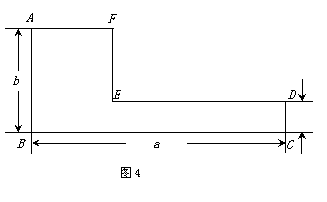
23)可量出AF边或DE边的长,(1)当AF=n时,S=bn+(a-n)·m=bn+am-mn
(2) 当DE=n时,S=mn+(a-n)·b=ab-bnm+mn
24)
|
含有一个相同字母的两个一次二项式相乘 |
乘法展开 |
得到的乘积 |
||
|
二次项 |
一次项 |
常数项 |
||
|
(x+2)(x+3) |
x2 |
5x |
6 |
x2+5x+6 |
|
(x+2)(x-3) |
x2 |
-x |
-6 |
x2+5x+6 |
|
(x-2)(x+3) |
x2 |
x |
-6 |
x2+5x+6 |
|
(x-2)(x-3) |
x2 |
-5x |
6 |
x2+5x+6 |
|
(x+a)(x+b) |
x2 |
(a+b)x |
ab |
x2+(a+b)x+ab |
含有一个相同字母的两个一次二项式相乘,得是一个含有这个字母的二次三项式,其中一次项乘以一次是二次项,一次项乘以常数项(或常数项乘以一次项)是一次项,常数项乘以常数项是积的常数项.
如果两个一次项的系数是1,那么积的二次项的系数是1,两个常数项的和是一次项和系数,两个常数积的常数项.
25)C=3b2-a2b
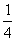
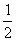
当a=-2,b= 时,C=3b2-a2b=
26) (1)-8x+3 -101 (2) 5.5
27)(1)81×89=7209=8×(8+1)×100+1×9
(2) 十位数字相同,个位数字的和等于10的两个两位数相乘,结果等于十位数字乘以比它大1的数字的积的100倍,再加上个位数字之积的和.
(3) (10n+a)(10n+b)=(10n)2+(a+b)·10n+ab=100n2+100n+ab=100×n·(n+1)+ab
28) (1)图b中的阴影部分的面积为 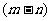 ;
;
(2)方法一: 方法二:
方法二:
(3)代数式 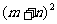 ,
, ,
, 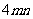 之间的关系为;
之间的关系为; =
= 
4)当 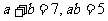 ,
, =
=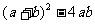 =
= .
.
27.观察下面的几个算式,你发现了什么规律?
①16×14=224=1×(1+1)×100+6×4
②23×27=621=2×(2+1)×100+3×7
③32×38=1216=3×(3+1)×100+2×8
……
(1)按照上面的规律,仿照上面的书写格式,迅速写出81×89的结果.
(2)简单叙述以上所发现的规律.
(3)我们知道(x+a)(x+b)=x2+(a+b)x+ab请用上面等式证明上面所发现的规律.
(提示:可设这两个两位数分别是(10n+a)、(10n+b),其中a+b=10)
26.(1)先化简,再求值 5x(2x+1)-(2x+3)(5x-1),其中x=13
(2)解下列方程2(x+3)(3-x)+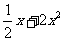 =17
=17
24、把下表中含有一个相同字母的两个一次二项式相乘的过程填写在相应的栏目中,观察所得乘积的二次项系数,一次项系数,常数项是怎么样确定的,并说出你得到的怎样的规律
|
含有一个相同字母的两个一次二项式相乘 |
乘法展开 |
得到的乘积 |
||
|
二次项 |
一次项 |
常数项 |
||
|
(x+2)(x+3) |
|
|
|
|
|
(x+2)(x-3) |
|
|
|
|
|
(x-2)(x+3) |
|
|
|
|
|
(x-2)(x-3) |
|
|
|
|
|
(x+a)(x+b) |
|
|
|
|
23.小颖要计算一个L形花坛的面积,在动手测量前她依花坛形状画了如下示意图,并用字母表示了将要测量的边长(如图4所标示),她在列式进行面积计算时,发现还需要再测量一条边的长度,你认为她还需测哪条边的长度?请你在图中标出来,并用字母n表示,然后再求出这个花坛的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com