
2.分式的约分
剖析:(1)如果分式的分子、分母都是单项式,就直接约去分子、分母的公因式,即分子、分母系数的最大公约数,相同字母的最低次幂;
(2)如果分子、分母都是多项式,就先分解因式,找出公因式再进行约分.
注:要牢记分子、分母都是乘积形式时,才能进行约分;约分要彻底,即约去公因式后为最简形式.
例题精讲
例1 (经典回放)写出一个含有字母x的分式:______________.(要求:不论x取任何实数,该分式都有意义,且分式的值为负)
思路解析:这是一道开放性试题,解题的关键是正确理解分式的概念和有意义的条件,首先找出符合条件的字母,由于x本身取任意实数,所以当分母取ax2n+b(a、b同号且n是正整数)时,ax2n+b≠0.因此分母可以用x2+1,3x2+2,-2x2-5等来表示,而对于分子,由于分式的值为负,因此也可用ax2n+b来选取.但要注意分子、分母异号,分式要写成最简形式.
答案:如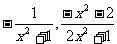 (答案不唯一)
(答案不唯一)
解题关键:准确理解分式的意义,含有字母x的分式的分母不等于零、满足ax2n+b≠0(a、b同号且n是正整数).
提高训练 若分式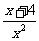 的值为正数,则x的取值范围是( )
的值为正数,则x的取值范围是( )
A.x>0 B.x>-4 C.x≠0 D.x>-4且x≠0
思路解析:x2为非负数,故要使分式的值为正数,需分子x+4大于零且 x≠0.
答案:D
例2 若 的值为零,则x的值是( )
的值为零,则x的值是( )
A.±1 B.1 C.-1 D.不存在
思路解析: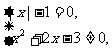 解得x=-1.
解得x=-1.
答案:C
解题关键:分式的值为零,必须同时满足两个条件:一是分子等于零;二是分母不等于零.
黑色陷阱:若只考虑分子等于0,则会错选A.因此当分式的值为零时,求字母的取值不能只考虑分子,还必须考虑分母.
提高训练1 若分式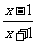 的值为零,则x的值为____________.
的值为零,则x的值为____________.
思路解析:分式的值为零,即分子x-1=0且分母x+1≠0.
答案:1
提高训练2 当m=__________时,分式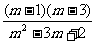 的值为0.
的值为0.
思路解析:令(m-1)(m-3)=0,得 m=1或m=3.
当m=1时,m2-3m+2=12-3×1+2=0;
当m=3时,m2-3m+2=32-3×3+2=2≠0.
所以当m=3时,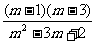 =0.
=0.
答案:3
例3 小明说:“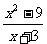 可以化简为x-3,所以
可以化简为x-3,所以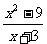 应该是整式.”你认为他的说法正确吗?说明理由.
应该是整式.”你认为他的说法正确吗?说明理由.
思路解析:这里的化简即约分,依据是分式的基本性质,在分式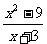 中,字母x的取值范围是x≠-3,而在x-3中x的取值范围是任意实数.
中,字母x的取值范围是x≠-3,而在x-3中x的取值范围是任意实数.
答案:不正确,化简后x的取值范围不同,因此x-3不能代替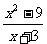 .
.
解题关键:在分式的约分中,默认的是字母的取值使分母不等于零;而在整式中,字母可取任意实数.
提高训练1 下列分式的变形是否正确?为什么?
(1)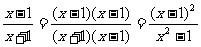 ;
;
(2)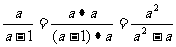 .
.
思路解析:分式的基本性质:分子、分母都乘以(或除以)同一个不等于零的整式,分式的值不变.在以上变形中,没有指明(x-1)和a不为零.
答案:都不正确,因为无法保证(1)中分子、分母同乘以的x-1和(2)中的a不为零.
提高训练2 下列分式变形是否正确?为什么?
(1)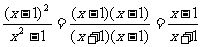 ;
;
(2)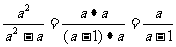 .
.
思路解析:两个变形也是利用分式的基本性质,原来的两个分式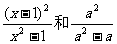 中隐含了x-1≠0和a≠0,故变形正确.
中隐含了x-1≠0和a≠0,故变形正确.
答案:变形正确,因为原分式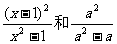 中隐含了x-1≠0和?a≠0的条件,可以进行约分.
中隐含了x-1≠0和?a≠0的条件,可以进行约分.
提高训练3 化简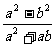 的结果是( )
的结果是( )
A.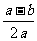 B.
B.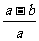 C.
C.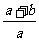 D.
D.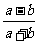
思路解析:先将原式分解因式化成积的形式, .
.
答案:B
课外讨论
问题 “因为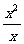 =x,而x取任意实数都有意义,所以使分式
=x,而x取任意实数都有意义,所以使分式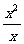 有意义的条件是x为任意实数”.你认为这种说法对吗?为什么?
有意义的条件是x为任意实数”.你认为这种说法对吗?为什么?
从分式在什么时候有意义的方面来考虑.
探究:因为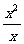 =x应用了分式的基本性质:分子、分母同除以不为0的整式x,分式的值不变,所以,这里要使得两式相等的首要条件是x≠0.也就是说没有x≠0这个条件,相等是无从谈起的.所以这种说法不对,要使
=x应用了分式的基本性质:分子、分母同除以不为0的整式x,分式的值不变,所以,这里要使得两式相等的首要条件是x≠0.也就是说没有x≠0这个条件,相等是无从谈起的.所以这种说法不对,要使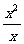 有意义,则x≠0.
有意义,则x≠0.
自我训练
达标训练
1.分式的意义与分式的值
剖析:(1)分式有意义是指分母不等于零,与分子的取值无关.
(2)分式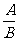 ,当A=0且B≠0时,分式的值为零;
,当A=0且B≠0时,分式的值为零;
当A>0,B>0或A<0,B<0(即A与B同号)时,分式的值为正;
当A>0,B<0或A<0,B>0(即A与B异号)时,分式的值为负.
因此在学习过程中要及时回顾方程和不等式的有关知识.
4.分式的通分
指把几个异分母的分式分别化成与原来的分式___________的___________的分式.分式通分的根据是___________.通常取各分母的所有因式的___________作公分母,这样的公分母,叫做最简公分母.
答案:相等 同分母 分式的基本性质 最高次幂的积
知识导学
学习本节应先回顾小学分数的知识,通过类比、猜想,学习分式的概念和性质.
分式约分和通分的依据是分式的基本性质,通分和约分实质上是一种恒等变形,它对于学习后面的分式运算和分式方程是十分重要的.
分式的符号变化规律要引起注意,其表现形式如下:
(1)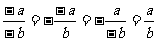 ;
;
(2)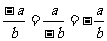 ;
;
(3)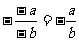 .
.
但要注意下面的错误: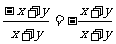 =-1是错误的,应该是
=-1是错误的,应该是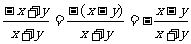 .
.
难点突破
3.分式的约分
指把一个分式的__________与__________的__________约去.分式约分的根据是___________.
分式约分的主要步骤是:
(1)把分式的分子与分母___________;(2)约去分子与分母的___________.
答案:分子 分母 公因式 分式的基本性质 化为积的形式 公因式
2.分式的基本性质
分式的分子与分母都乘以(或除以)___________,分式的值不变.
答案:.同一个不等于零的整式
1.分式的有关概念
(1)用A、B表示两个整式,A÷B可以表示成___________的形式;如果B中___________,式子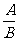 就叫做分式.
就叫做分式.
(2)若分式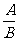 有意义,则B___________.
有意义,则B___________.
(3)若分式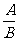 无意义,则B___________.
无意义,则B___________.
(4)若分式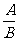 =0,则A___________,且B___________.
=0,则A___________,且B___________.
答案:(1)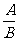 含有字母
含有字母
(2)≠0
(3)=0
(4)=0 ≠0
16.1 分 式
把握要点
6.通过学习,能获得学习数学知识的常用方法,感受数学学习的价值.
知识结构
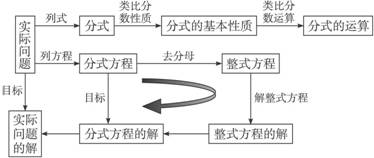
5.能解决一些与分式、分式方程有关的实际问题,具有一定的分析问题、解决问题的能力和应用意识.
4.会解可化为一元一次方程的分式方程(方程中分式不超过2个);会检验分式方程的根.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com