1. 三角形的三边长分别为6,8,10，它的最短边上的高为(　 　)

A. 6　　　　 B. 4.5　　　　 C. 2.4　　　　　 D. 8

25．(12分)台风是一种自然灾害，它以台风中心为圆心在周围数十千米范围内形成气旋风暴，有极强的破坏力，据气象观测，距沿海某城市A的正南方向220km的B处有一台风中心．其中心最大风力为12级，每离台风中心20km，风力就会减弱一级，该台风中心现在正以15km/h的速度沿北偏东30°方向往C移动，且台风中心风力不变，如图14-10，若城市所受风力达到或超过4级，则称为受台风影响．

　 (1)该城市是否会受到这次台风的影响？请说明理由；

　 (2)若会受台风影响，那么台风影响该城市的持续时间有多长？该城市受到台风影响的最大风力为几级？

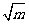24．(12分)清朝康熙皇帝是我国历史上对数学很有兴趣的帝王．近日，西安发现了他的数学专著，其中有一文《积求勾股法》，它对“三边长为3、4、5的整数倍的直角三角形，已知面积求边长”这一问题提出了解法：“若所设者为积数(面积)，以积率六除之，平方开之得数，再以勾股弦各率乘之，即得勾股弦之数”．用现在的数学语言表述是：“若直角三角形的三边长分别为3、4、5的整数倍，设其面积为S，则第一步：＝m；第二步：=k；第三步：分别用3、4、5乘以k，得三边长”．

　 (1)当面积S等于150时，请用康熙的“积求勾股法”求出这个直角三角形的三边长；

　 (2)你能证明“积求勾股法”的正确性吗？请写出证明过程．

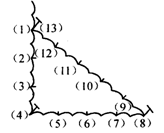
23．(8分)古埃及人用下面方法画直角：把一根长绳打上等距离的13个结，然后用桩钉成如图所示的一个三角形，其中一个角便是直角，请说明这种做法的根据．

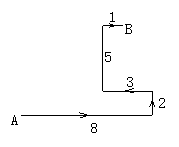
22．(10分)如图所示，某人到一个荒岛上去探宝，在A处登陆后，往东走8km，又往北走2km，遇到障碍后又往西走3km，再折向北方走到5km处往东一拐，仅1km就找到了宝藏，问：登陆点(A处)到宝藏埋藏点(B处)的直线距离是多少？

21．(8分)如图所示，四边形ABCD中，AB=4，BC=3，AD=13，CD=12，∠B=90°，求该四边形的面积．

19．(8分)已知一个矩形的两邻边之比为3：4，且周长为42cm，求矩形的对角线长．20．(8分)求图中字母所代表的正方形面积．

18．已知Rt△ABC中，∠C=90°，若a+b=14，c=10，则Rt△ABC的面积是_______．

17．有一长、宽、高分别为5cm、4cm、3cm的木箱，在它里面放入一根细木条(木条的粗细、形变忽略不计)，要求木条不能露出木箱，请你算一算，能放入的细木条的最大长度是_________cm．

16．能够成为直角三角形三条边长的三个正整数，称为勾股数，试写出两种勾股数_______．