1．12，8，6　 　　　　　　　　　　　　　　2．矩形，扇形，矩形　

28．(本题6分)灯塔A在灯塔B的南偏东60°方向上，A、B相距30海里，轮船C在B的正南方向，在灯塔A的南偏西60°方向上，通过画图(用1个单位代表10海里)确定轮船C的位置，求∠BAC和∠ACB的度数，并求出轮船C与灯塔B的距离．

第四章图形认识初步自主学习达标检测

27．根据题意填空：((1)-(2)每小问1分，(3)每小问2分，共6分)

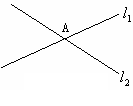
(1)l₁与l₂是同一平面内两条相交直线，他们有一个交点，如果在这个平面内，再画第三条直线l₃，那么这三条直线最多有　　　 ____________个交点．

(2)如果在(1)的基础上在这个平面内再画第四条直线l₄，那么这四条直线最多可有______________个交点．

(3)由(1)(2)我们可以猜想：在同一平面内，6条直线最多可有_________个交点，n(n＞1)条直线最多可有__________条交点．(用含有n的代数式表示)

26．(本题6分)如图，(1)已知∠AOB为直角，∠AOC为锐角，OE平分∠BOC，OF平分∠AOC，求∠EOF的度数；

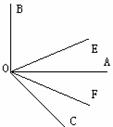　 (2)若将(1)中的条件“∠AOB为直角”改为“∠AOB为任意一个角”，则∠AOB与∠EOF的大小关系如何？发现结论并说明理由．

25．(本题6分)已知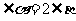，的余角的3倍等于的补角，求、的度数．

24．(本题6分)已知：如图，点C是线段AB上一点，且3AC=2AB．D是AB的中点，E是CB的中点，DE=6，求：(1)AB的长 ；(2)求AD：CB．

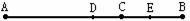
23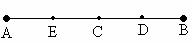．(本题4分)AB是一段火车行驶路线图，图中字母表示的5个点表示5个车站，在这段路线上往返行车，需印制几种车票？

22．(本题4分)如图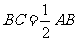，，D为AC的中点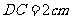，，求AB的长．

21．(本题6分)如图，直线AB与CD相交于点O，OE⊥CD，OF⊥AB，∠DOF=65°．

求：(1)∠BOE的度数；

(2)∠AOC的度数．

20．(本题4分)如图，已知AOB是一条直线，∠1=∠2，∠3=∠4，OF⊥AB．则

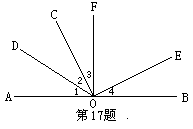(1)∠AOC的补角是　　　　　　　　 ；

(2)　　　　　　 是∠AOC的余角；

(3)∠DOC的余角是　　　　　 　　；

(4)∠COF的补角是　　　　　　　 ．