
(1)认识方位:
正东、正南、正西、正北、东南、
西南、西北、东北。
(2)找方位角:
ⅰ乙地对甲地的方位角 ⅱ甲地对乙地的方位角
例3:选择题:
(1)A看B的方向是北偏东21°,那么B看A的方向( )
 A:南偏东69° B:南偏西69° C:南偏东21° D:南偏西21°
A:南偏东69° B:南偏西69° C:南偏东21° D:南偏西21°
(2)如图,下列说法中错误的是( )
A: OC的方向是北偏东60°
B: OC的方向是南偏东60°
C: OB的方向是西南方向
D: OA的方向是北偏西22°
(3)在点O 北偏西60°的某处有一点A,在点O南偏西20°的某处有一点B,则∠AOB的度数是( ) A:100° B:70° C:180° D:140°
 例4:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
例4:如图.货轮O在航行过程中,发现灯塔A在它南偏东60°的方向上,同时,在它北偏东40°,南偏西10°,西北(即北偏西45°)方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法画出表示客轮B,货轮C和海岛D方向的射线.
如图∠1 与∠2互余,∠3 与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?


得出结论:∠2=∠4
理由:∵ ∠1 +∠2=90°, ∠3 +∠4=90°
∴ ∠2=90°-∠1 , ∠4=90°- ∠3
∵ ∠1 =∠3
∴ 90°-∠1 =90°- ∠3
即:∠2 =∠4
余角性质:等角的 相等
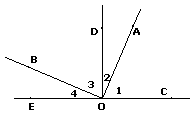 例2: 如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?
例2: 如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?
解:∠1=∠3
∵ ∠1+∠2= ∠COD=90°
∠3+∠2= ∠AOB=90°
∴ ∠1=∠3 (等角的余角相等)
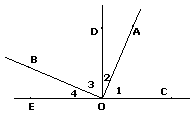 如图∠1 与∠2互余,∠3
与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?(请模仿补角的性质进行说理)
如图∠1 与∠2互余,∠3
与∠4互余 ,如果∠1=∠3,那么∠2与∠4相等吗?为什么?(请模仿补角的性质进行说理)


|
余角性质:等角的 相等
例2: 如图,∠AOB=90°,∠COD=∠EOD=90°,C,O,E在一条直线上,且∠2=∠4,请说出∠1与∠3之间的关系?并试着说明理由?
例1、如图, ∠1与∠2互补,∠3与∠4互补, ∠1= ∠3,那么∠2与∠4相等吗?为什么?

分析:(1)∠1与∠2互补,∠2等于什么?∠3与∠4互补,∠4等于什么?
∠2=1800 - ,∠4=1800 - 。
(2)当∠1= ∠3时,∠2与∠4有什么关系?为什么?
解:∠2=∠4 理由:∵∠1与∠2互补,∠3与∠4互补
∴∠1+∠2=1800, ,∠3+∠4=1800,
∴∠2=1800-∠1,∠4=1800-∠3
又∵∠1= ∠3
∴1800-∠1=1800-∠3(等量减等量,差相等)
即 ∠2=∠4
上面的结论,用文字怎么叙述?
补角的性质:等角的 相等。
28.作图略,30海里。
27.(1)3;(2)6;(3)15;(4)
26.(1)45°(2)
25.
24.(1)18;(2)3︰2
23.20种
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com