
6.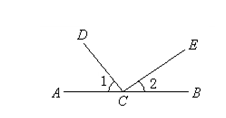
 如图,A、B、C在一直线上,已知
如图,A、B、C在一直线上,已知 1=53°,
1=53°, 2=37°.CD与CE垂直吗?
2=37°.CD与CE垂直吗?
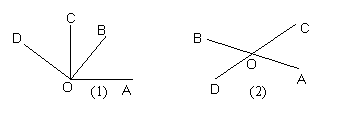
5.由图形填空 :
∠AOC=______+______ ;
∠AOC-∠AOB =_________ ;
∠COD= ∠AOD-_______ ;
∠BOC= _____- ∠COD ;
∠AOB+∠COD=_____-______.
4.计算下列各题:
(1)23°30′=____°;13.6°=____°____′;
(2)52°45′-32°46′=____°____′;
(3)18.3°+26°34′=____°____′.
6、方位角
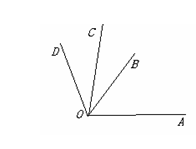
 (4)如图,OA方向表示什么?OB方向表示什么?OC方向表示什么?
(4)如图,OA方向表示什么?OB方向表示什么?OC方向表示什么?
5、余角和补角
(1)定义:如果两个角的和等于900,就说这两个角互为余角。
如果两个角的和等于1800,就说这两个角互为补角。
注意:余角和补角是两个角之间的关系;只与数量有有关,而与位置无关。
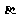
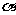 (2)已知∠ =47023′,则它的余角 = ,补角 = .
(2)已知∠ =47023′,则它的余角 = ,补角 = .
(2)余角和补角的性质
同角(等角)的余角相等。
同角(等角)的补角相等。
(3)如图(1),∠AOC= ∠BOD=900,则∠AOB= ∠DOC,为什么?(2)直线AB与直线CD相交于点O,则∠AOC= ∠DOB,为什么?
4、角的平分线
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线。表示为
∠AOC= ∠COB
 或∠ AOC=∠COB= 1/2∠AOB
或∠ AOC=∠COB= 1/2∠AOB
或2∠ AOC=2∠COB= ∠AOB
3、角的比较
比较角的方法:度量法和叠合法。
(1)根据图形回答下列问题:
(1) ∠AOC是哪两个角的和?
(2) ∠AOB是哪两个两个角的差?
2、角的度量
 10=60′;1′=60′′.
10=60′;1′=60′′.
3.情感、态度与价值观
在探索知识之间的相互联系及应用的过程中,体验推理的意义,获取学习的经验.
教学重点:立体图形与平面图形的互相转化,及一些重要的概念、性质等.
解决方法:通过观察、测量、折叠、模型制作与团设计等活动,发展空间观念,自然就加强了对概念及其性质的理解和掌握.
教学难点:建立和发展空间观念;对图形的表示方法,对几何语言的认识与运用.
解决办法:通过多实践操作;加强对几何语言的运用.
教学方法:引导式.
教具准备:投影仪.
教学安排:3课时.
教学过程设计:
|
教 学 过 程 |
修 改 与 备 注 |
|
一、导入 回忆一下,这一章我们都学习了哪些知识呢? 教师可以先给出本章的知识结构图:(投影仪)  (教师先给一段时间思考,同学之间可以相互交流.) 二、知识回顾 教师提问:本章的主要内容有哪些呢? 师:(概述) 本章的主要内容是图形的初步认识,从生活周围熟悉的物体入手,对物体的形状的认识从感性逐步上升到抽象的几何图形.通过从不同方向看立体图形和展开立体图形,初步认识立体图形与平面图形的联系.在此基础上,认识一些简单的平面图形--直线、射线、线段和角. 师:我们来对各个小节的知识回顾一下: 第一节: 多姿多彩的图形:通过多姿多彩的图形引入几何图形,使我们认识立体图形、平面图形,通过三视图我们可以把立体图形转化为平面图形来研究和处理,也可以把立体图形展开为平面图形;几何体也简称为体,包围体的是面,面面相交为线,线线相交为点;点动成线,线动成面,面动成体,几何图形都是由点、线、面、体组成的,点是构成图形的基本元素. 举例:广场礼花在夜空中留下的图形,你是否看到了点动成线?在电视中看到收割机在麦田中收割小麦,你是否看到了线动成面? 第二节: 1.直线、射线、线段的区别与联系:从图形上看,直线、射线可以看做是线段向两边或一边无限延伸得到的,或者也可以看做射线、线段是直线的一部分;线段有两个端点,射线有一个端点,直线没有端点;线段可以度量,直线、射线不能度量. 2.直线、线段性质: 经过两点有一条直线,并且只有一条直线;或者说两点确定一条直线; 两点的所有连线中,线段最短;简单说:两点之间,线段最短. 3.线段中点:把一条线段分成两条相等的线段的点叫线段中点,如图: 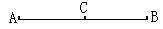 若点C是线段AB的中点,则有(1)AC=BC= 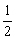 AB 或(2)AB=2AC=2BC,反之,若有(1)式或(2)式成立,亦能说明点C是线段AB的中点. AB 或(2)AB=2AC=2BC,反之,若有(1)式或(2)式成立,亦能说明点C是线段AB的中点.4.关于线段的计算:两条线段长度相等,这两条线段称为相等的线段,记作AB=CD,平面几何中线段的计算结果仍为一条线段.即使不知线段具体的长度也可以作计算. 例:如图:AB+BC=AC,或说:AC-AB=BC  第三节: 1.角的意义:有公共端点的两条射线组成的图形叫做角,公共端点是角的顶点,这两条射线是角的两条边,角也可以看做由一条射线绕着它的端点旋转而形成的图形. 2.角的度量:1°=60′ 1′=60″ 1周角=360° 1平角=180° 1直角=90° 第四节: 1.角的大小的比较:(1)叠合法,使两个角的顶点及一边重合,另一边在重合边的同旁进行比较;(2)度量法. 2.角的平分线:从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线.如图:OC平分∠AOB,则(1)∠AOC=∠BOC= 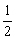 ∠AOB或(2)2∠AOC =2∠BOC =∠AOB. ∠AOB或(2)2∠AOC =2∠BOC =∠AOB.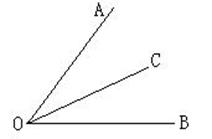 3.有关角的运算: 举例说明:如图,∠AOC+∠BOC=∠AOB,∠AOB-∠AOC=∠BOC 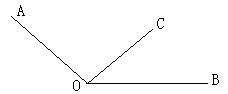 特殊情况,如果两个角的和等于直角,就说这两个角互为余角,即其中一个是另一个的余角;如果两个角的和等于平角,就说这两个角互为补角,即其中一个是另一个的补角;等角的余角相等,等角的补角相等. 三、例题讲解 例1 如图3-162所示,讲台上放着一本书,书上放着一个粉笔盒,指出右边三个平面图形分别是左边立体图形的哪个视图. 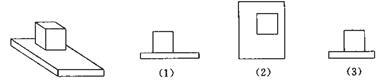 图3-162 解:(1)左视图,(2)俯视图,(3)正视图 例2 (1)如图3-163所示,上面是一些具体的物体,下面是一些立体图形,试找出与下面立体图形相类似的物体. (2)如图3-164所示,写出图中各立体图形的名称.  图3-163 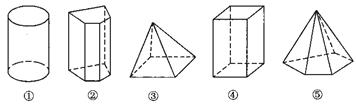 图3-164 解:(1)①与d类似,②与c类似,③与a类似,④与b类似. (2)①圆柱,②五棱柱,③四棱锥,④五棱锥. 例3 (1)过一个已知点的直线有多少条? (2)过两个已知点的直线有多少条? (3)过三个已知点的直线有多少条? (4)经过平面上三点A,B,C中的每两点可以画多少条直线? (5)根据(4)的结论,猜想经过平面上四点A,B,C,D中的任意两点画直线,会有什么样的结果?如果不能画,请简要说明理由;如果能画,请画出图来. 解:(1)过一点可以画无数条直线. (2)过两点可以画惟一的一条直线. (3)过三个已知点不一定能画出直线. 当三个已知点在一条直线上时,可以画出一条直线; 当三个已知点不在一条直线上时,不能画出直线. (4)如图3-165所示,当A,B,C三点不共线时,过其中的每两点可以画一条直线,共可画出三条直线;当A,B,C三点在一条直线上时,经过每两点画出的直线重合为一条直线.  图3-165 (5)经过平面上四点中的任意两点画直线,一共有三种情况,如图3-166所示, 当A,B,C,D四点共线时,只能画出一条直线; 当A,B,C,D四点中有三点在同一直线上时,可以画出四条直线; 当A,B,C,D中不存在三点在同一直线上时,可以画出六条直线. 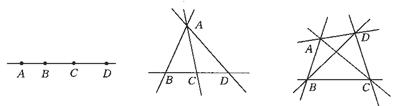 图3-166 例4 如图3-172所示,已知三点A,B,C,按照下列语句画出图形. (1)画直线AB; (2)画射线AC; (3)画线段BC. [分析]本题要求能根据几何语言规范而准确地画出图形,要做到这一点,关键是:第一,要读懂这些几何语句;第二,要抓住这些基本图形的共同特点及细微区别.如直线、射线、线段的共同特点是都是笔直的线,不同的是:线段有两个端点,不能延伸;射线有一个端点,向一方无限延伸;直线没有端点,向两方无限延伸.它们的表示方法:线段是用它的两个端点的大写字母来表示的;射线是用它的端点和射线上另外一个任意点的大写字母来表示的,且端的字母要写在前面;直线是用它上面的任意两个点的大写字母来表示的.弄清楚这几点,图就不难画出了. 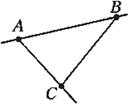 图3-172 解:如图3-172所示,直线AB、射线AC、线段BC即为所求. 例5 如图3-173所示,回答下列问题. 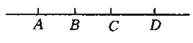 图3-173 (1)图中有几条直线?用字母表示出来; (2)图中有几条射线?用字母表示出来; (3)图中有几条线段?用字母表示出来. [分析]掌握线段、直线的区别与联系,射线的方向性,线段的无向性,就可以解决这类问题. 解:(1)图中有1条直线,表示为直线AD(或直线AB,AC,BD,BC,CD); (2)共有8条射线,能用字母表示的有射线AB,AC,AD,BC,BD,CD,不能用字母表示的有2条, (3)共有6条线段,表示为线段AB,AC,AD,BC,BD,CD. 例6 如图3-184所示的是两块三角板. (1)用叠合法比较∠1,∠  ,∠2的大小; ,∠2的大小;(2)量出各角的度数,并把图中6个角从小到大排列,然后用“<”或“=”号连接. [分析]叠合法就是把两个角的一边重合,根据另一边的位置就可以比较出角的大小. 解:(1)如图3-184所示 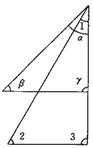 图3-184 把两块三角板叠在一起,可得∠1<∠  ,用同样的方法可得∠ ,用同样的方法可得∠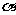 <∠2, <∠2,所以∠1<∠ 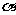 ∠2. ∠2.(2)用量角器量出各角的度数分别是∠1=30°, ∠2=60°, ∠3=90°, ∠ 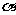 =45°, ∠ =45°, ∠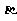 =45°, ∠ =45°, ∠ =90°, =90°,∴∠1<∠ 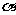 =∠ =∠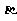 <∠2<∠3=∠ <∠2<∠3=∠ . .例7 (1)计算:①27°42′30″+1070′;②63°36′-36.36°. (2)用度、分、秒表示48.12°. (3)用度表示50°7′30″. [分析]在复名数与单名数的加减运算中,参加运算的各个名数需化成相应的同一名数(同为复名数或同为单名数).进行角度的单位换算时,因为是60进制,所以度化分、分化秒要乘以60,秒化分、分化度要除以60(即从高一级单位化为低一级单位要乘以60,从低一级单位化为高一级单位要除以60). 解:(1)①27°42′30″+1070′=27°42′30″+17°50′=45°32′30″. ②63°36′-36.36°=63°36′-36°21′36″=63°35′60″-36°21′36″ =27°14′24″ 或63°36′-36.36°=63°36′-36°21.6′=27°14.4′=27°14′24″. (2)∵48.12°=48°+0.12°,0.12°=60′×0.12=7.2′=7′+0.2′, 0.2′=60″×0.2=12″,∴48.12°=48°7′12″. (3)∵50°7′30″=50°+7′+30″=50°+7′+0.5′=50°+7.5′ =50°+0.125°=50.125°. ∴50°7′30″=50.125°. 例8 任意画一个角. (1)用量角器量出它的度数,然后计算它的余角与补角的度数;(精确到度) (2)用三角板画出它的余角及补角,再用量角器量出余角及补角的度数.(精确到度)  图3-186 解:(1)任意画一个角∠ABC(如图3-186(1)所示), 用量角器量得∠ABC=38°, 那么∠ABC的余角是度数是90°-∠ABC=90°-38°=52°; ∠ABC的补角的度数是180°-∠ABC=180°-38°=142°. (2)如图3-186(2)所示,用三角板的直角顶点对准∠ABC的顶点B, 使三角板的一条直角边与BC重合, 画出∠CBD=90°(BA在∠CBD的内部), 则∠ABD是∠ABC的余角, 再用量角器量得∠ABD=52°. 反向延长BC,得射线BE, 则∠ABE是∠ABC的补角, 再用量角器量得∠ABE=142°. [注意]此题中任意画的角∠ABC必须是锐角,否则它没有余角. 例9 小明从A点出发,向北偏西33°方向走33 m到B点,小林从A点出发,向北偏东20°方向走了6.6 m到C点,试画图确定A,B,C三点的位置(1cm表示3m),并从图上求出点B,C的实际距离. 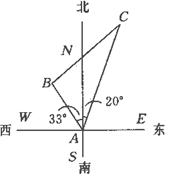 图3-187 解:①如图3-187所示,任取一点A,经过点A画一条东西方向的直线WE和一条南北方向的直线NS(两条直线相交成90°角). ②在∠NAW内作∠NAB=33°,量取AB=1.1cm. ③在∠NAE内作∠NAC=20°, 量取AC=2.2cm. ④连接BC,量得BC=1.8cm, ∴BC的实际距离是5.4m. 四、布置作业 1. 已知平面内有四个点 A、B、C、D,过其中任意两点画直线,最少可画多少条直线,最多可画多少条直线?画出图来并说明理由. 2.已知点C是线段AB的中点,点D是线段BC的中点,CD=2.5厘米,请你求出线段AB、AC、AD、BD的长各为多少? 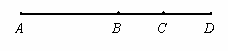 3.已知线段AB=4厘米,延长AB到C,使B C=2AB,取AC的中点P,求PB的长. 4.计算下列各题: (1)23°30′=____°;13.6°=____°____′; (2)52°45′-32°46′=____°____′; (3)18.3°+26°34′=____°____′. 5.由图形填空 : ∠AOC=______+______ ; ∠AOC-∠AOB =_________ ; ∠COD= ∠AOD-_______ ; ∠BOC= _____- ∠COD ; ∠AOB+∠COD=_____-______. 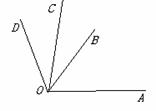 6.如图,A、B、C在一直线上,已知  1=53°, 1=53°, 2=37°.CD与CE垂直吗? 2=37°.CD与CE垂直吗?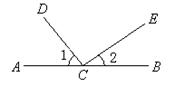 7.如图,经过直线a外一点p的4条直线中,与直线a平行的直线有___,共有__条. 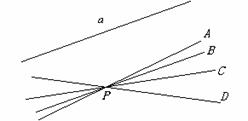 8.如图,如果AB∥CD,那么  A与 A与 C__________. C__________.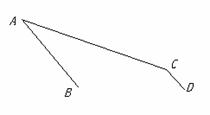 |
|
教学反思:
2.过程与方法
经历相关内容的归纳、总结,巩固对图形的直观认识,了解图形的分割和组合,探索学习空间与图形的方法;
通过实验、操作,提高对图形的认识和动手能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com