24．　 (1)；　　　　　　　　　　　　　　　　　　　　　　　 　

　(2)－x²+2x　 ，1， ；　　　　　　　　 　　

23． (1) 25 ；　　　　　　　　　　　　　　　　　　　　　　　 　

(2) 50；　　画对条形统计图　　　　　　　　　　　　 　

(3)5人；

20．(1)∵AB是⊙O直径，∴∠ACB=Rt∠．∴sin∠BAC=．　 　

(2)∵OE⊥AC,O是⊙O的圆心, ∴E是AC中点．∴OE＝BC=．　 　

(3)∵AC＝=4， ∴tan∠ADC= tan∠ABC=．　　　 　

21,　 (1)　 C　　 (2) 　没有考虑

(3)

22,解(1)当x30时,设函数关系式为y=kx+b

则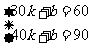-　 解得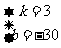　　 所以y=3x-30

(2)4月份上网20小时,应付上网费60元

(3) 由75=3x-30解得x=35,所以5月份上网35个小时.

19．答案不唯一．只要符合要求，画对一个给4分，画对两个给8分．　　　　

18．(1)；　　　　　　　　　　　　　

　(2)列对表格或画对树状图；　　　　　　　　　

　　两次都取到欢欢的概率为．　　　　　　　　

17．添加条件例举：AD＝BC；OC＝OD；∠C＝∠D；∠CAO＝∠DBC等.　　 　

证明例举(以添加条件AD＝BC为例)：

∵ AB=AB，∠1＝∠2，BC＝AD，　　　　　　　　　 　　 　

∴ △ABC≌△BAD．　　　　　　　　　　　　　　　　 　　　

　　　　 ∴ AC=BD．　　　　　　　　　　　　　　 　　　　　　　　　

16. 　(1)解：原式＝1+3－＝　　　　　　　　　　　　　　　　　　　　　　　　 　

(2)解：愿方程可化为：x＝3(x－2 )　　　　　　　　　　　　　　 　　

　　　　　　　　　　 x＝3　　　　　　　　　　　　　　　　　 　　

经检验 ：x＝3 是原方程的解．　　　　　　　　　　　　　　 　

11．X≠6 ； 　　12． 2；　13．8；　 　　14．　 65°；　15．96 ；　　　　 　

25.如图,平面直角坐标系中,直线AB与轴,轴分别交于A(3,0),B(0,)两点, ,点C为线段AB上的一动点,过点C作CD⊥轴于点D.

(1)求直线AB的解析式;

(2)若S_梯形OBCD＝,求点C的坐标;

(3)在第一象限内是否存在点P,使得以P,O,B为顶点的

三角形与△OBA相似.若存在,请求出所有符合条件

的点P的坐标;若不存在,请说明理由.(做出一种答案即可)

茂名市第十中学中考综合训练数学试卷(三)

24.初三(1)班数学兴趣小组在社会实践活动中，进行了如下的课题研究：用一定长度的铝合金材料,将它设计成外观为长方形的三种框架，使长方形框架面积最大.

小组讨论后,同学们做了以下三种试验:　　　　　　　　　

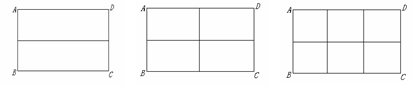
图案(1)　　　　　　 图案(2)　　　　　　　 图案(3)　　　　　

请根据以上图案回答下列问题:

(1)在图案(1)中,如果铝合金材料总长度(图中所有黑线的长度和)为6米,当AB为1米,

长方形框架ABCD的面积是　 　　　　　m²;

(2)在图案(2)中,如果铝合金材料总长度为6米,设AB为米,长方形框架ABCD的面积为S＝　 　　　(用含的代数式表示)；当AB＝　 　　　时米, 长方形框架ABCD的面积S最大;

在图案(3)中,如果铝合金材料总长度为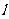米, 设AB为米,当AB是多少米时, 长方形框架ABCD的面积S最大.