
9. 右边给出的是2007年3月份的日历表,任意
右边给出的是2007年3月份的日历表,任意
圈出一竖列上相邻的三个数,请你运用方程思想来研
究,发现这三个数的和不可能是( )
(A) 69 (B) 54 (C) 27 (D)40
8.如图:圆的直径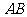 垂直弦
垂直弦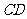 于
于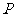 ,且
,且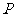 是半径
是半径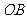 的中点,
的中点,
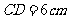 ,则直径AB的长是 ( )
,则直径AB的长是 ( )
(A)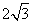 (B)
(B)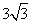 (C)
(C)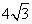 (D)
(D)
7. 如果四边形的对角线相等,且互相垂直平分,则它一定是( )
如果四边形的对角线相等,且互相垂直平分,则它一定是( )
(A) 矩形 (B) 菱形 (C)正方形 (D)等腰梯形
6.如图,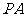 切⊙O于点
切⊙O于点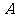 ,直线PBC经过点圆心
,直线PBC经过点圆心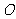 ,
,
若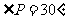 ,则∠ACB的度数为( ).
,则∠ACB的度数为( ).
(A)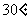 (B)
(B)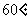 (C)
(C)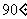 (D)
(D)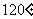
5.当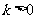 ,
,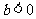 时,
时,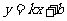 的图象经过 (
)
的图象经过 (
)
 (A) 第1、2、3象限
(B) 第2、3、4象限
(A) 第1、2、3象限
(B) 第2、3、4象限
(C) 第1、2、4象限 (D) 第1、3、4象限
4.二次函数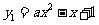 的图像与
的图像与 图像的形状、开口方向相同,只是位置不同,
图像的形状、开口方向相同,只是位置不同,
则二次函数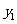 的顶点坐标是(
)
的顶点坐标是(
)
(A) (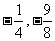 ) (B)
(
) (B)
(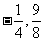 )
(C) (
)
(C) (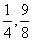 ) (D) (
) (D) (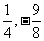 )
)
3.如图是由5个大小相同的正方体摆成的立方体图形,它的左视图是( )
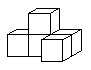
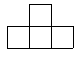
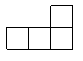
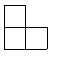
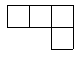
(A) (B) (C) (D)
2.下列关于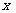 的一元二次方程中,有两个不相等的实数根的方程是(
)
的一元二次方程中,有两个不相等的实数根的方程是(
)
(A) (B)
(B)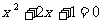
(C)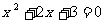 (D)
(D)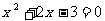
1.下列运算中,结果正确的是 ( )
(A) 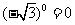 (B)
(B) 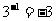 (C )
(C )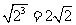 (D)
(D) 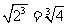
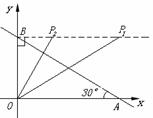
25.(1)直线AB解析式为:y=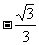 x+
x+ .
.
(2)方法一:设点C坐标为(x,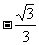 x+
x+ ),那么OD=x,CD=
),那么OD=x,CD=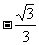 x+
x+ .
.
∴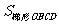 =
=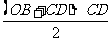 =
=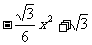 .
.
由题意: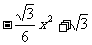 =
=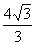 ,解得
,解得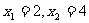 (舍去)
(舍去)
∴ C(2,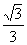 )
)
方法二:∵ 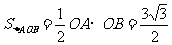 ,
,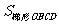 =
=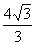 ,∴
,∴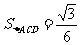 .
.
由OA= OB,得∠BAO=30°,AD=
OB,得∠BAO=30°,AD= CD.
CD.
∴ 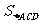 =
= CD×AD=
CD×AD=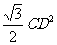 =
=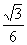 .可得CD=
.可得CD=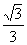 .
.
 ∴ AD=1,OD=2.∴C(2,
∴ AD=1,OD=2.∴C(2,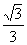 ).
).
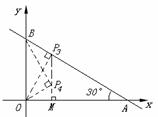
(3)当∠OBP=Rt∠时,如图
①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP= OB=3,
OB=3,
∴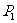 (3,
(3,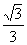 ).
).
②若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=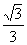 OB=1.
OB=1.
∴ (1,
(1, ).
).
当∠OPB=Rt∠时
③ 过点P作OP⊥BC于点P(如图),此时△PBO∽△OBA,∠BOP=∠BAO=30°
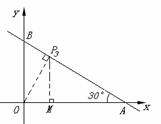 过点P作PM⊥OA于点M.
过点P作PM⊥OA于点M.
方法一: 在Rt△PBO中,BP= OB=
OB=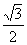 ,OP=
,OP= BP=
BP= .
.
∵ 在Rt△PMO中,∠OPM=30°,
∴ OM= OP=
OP=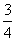 ;PM=
;PM= OM=
OM=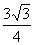 .∴
.∴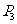 (
(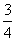 ,
,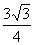 ).
).
 方法二:设P(x ,
方法二:设P(x ,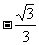 x+
x+ ),得OM=x ,PM=
),得OM=x ,PM=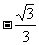 x+
x+
由∠BOP=∠BAO,得∠POM=∠ABO.
∵tan∠POM==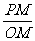 =
=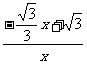 ,tan∠ABOC=
,tan∠ABOC=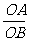 =
= .
.
∴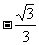 x+
x+ =
= x,解得x=
x,解得x=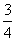 .此时,
.此时,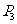 (
(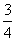 ,
,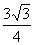 ).
).
④若△POB∽△OBA(如图),则∠OBP=∠BAO=30°,∠POM=30°.
∴ PM=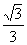 OM=
OM=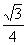 .
.
∴ 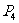 (
(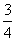 ,
,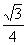 )(由对称性也可得到点
)(由对称性也可得到点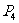 的坐标).
的坐标).
当∠OPB=Rt∠时,点P在x轴上,不符合要求.
综合得,符合条件的点有四个,分别是:
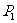 (3,
(3,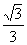 ),
), (1,
(1, ),
),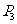 (
(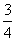 ,
,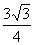 ),
),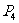 (
(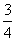 ,
,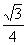 ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com