
24.解: (1)由图可知洗衣机的进水时间是4分钟,.清洗时洗衣机中的水量是40升
(2)①∵排水的时间是2分钟, 排水速度为每分钟19升,
∴排水结束时洗衣机中剩下的水量是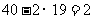 (升)
(升)
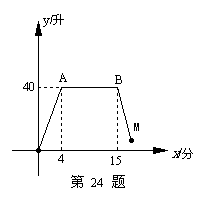 ② ∵
② ∵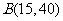 ,
,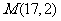
设 的函数表达式为
的函数表达式为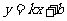
则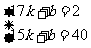 解这个方程组得,
解这个方程组得,

∴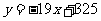 (
(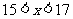 )
)
19. 解:在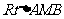 中,
中,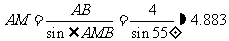
 ∵
∵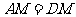 (6分),
(6分),
∴
答:D点到地面垂直的距离是 米.
米.
20 解:
(1)按要求作出梯形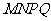
(2) 按要求作出梯形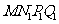
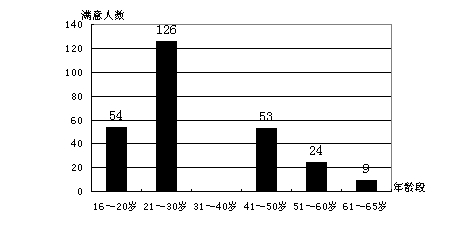
21解: (1) 被抽查的居民中,人数最多的年龄段是21~30岁
(2)总体印象感到满意的人数共有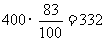 (人)
(人)
31~40岁年龄段总体印象感到满意的人数是
 (人)
(人)
22解:△CDB∽△CAD,设BC=x,CD2=CB·CA,即4=x(x+2)
解得:x=-1± (负值不合题意,舍去)
(负值不合题意,舍去)
所以,BC=-1+ 。
。
连接OD,则△OCD∽△ECB
∴ 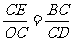 即
即 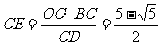
23,解:⑴设蓝球个数为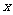 个
个
则由题意得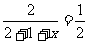
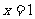
 答:蓝球有1个
答:蓝球有1个
--
--
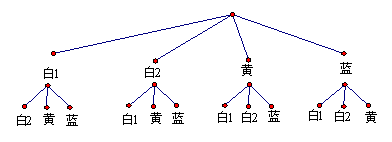
∴ 两次摸到都是白球的概率 =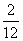 =
=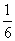
16.解:∵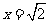
∴原式=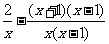 =
=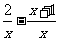 =
=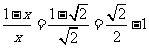
17 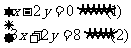
解:由(1)得, (3),
(3),
把(3)代入(2)式得, 解得,
解得,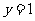
把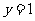 代入(3)得
代入(3)得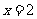 ∴原方程组的解是
∴原方程组的解是 
18解:设所租的车每天走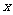 公里,依题意得,
公里,依题意得, 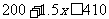
解锝, 答:最多可走140公里 .
答:最多可走140公里 .
13. 如 等
14. 6 15. 8
等
14. 6 15. 8
11.2,
12. 且
且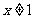
25. 如图在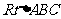 中,
中,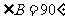 ,
,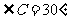 ,
,

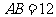 厘米,点P从点A出发沿线路AB-BC作匀速运动,点
厘米,点P从点A出发沿线路AB-BC作匀速运动,点
从AC的中点D同时出发沿线路DC-CB作匀速运动逐步
靠近点P, 设P,Q两点运动的速度分别为1厘米/秒、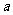 厘米/秒(
厘米/秒(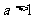 ),
),
它们在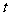 秒后于BC边上的某一点相遇.
秒后于BC边上的某一点相遇.
(1) 求出AC与BC的长度.
(2) 试问两点相遇时所在的E点会是BC的中点吗?为什么?
(3) 若以D,E,C为顶点的三角形与 相似,试分别求出
相似,试分别求出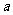 与
与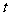 的值.(精确到0.1)
的值.(精确到0.1)
茂名市第十中学中考综合训练数学试卷(二)
24.某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、
清洗、排水时洗衣机中的水量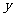 (升)与时间
(升)与时间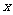 (分钟)之间的关系如折线图所示:
(分钟)之间的关系如折线图所示:
 根据图象解答下列问题:
根据图象解答下列问题:
(1)洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(2)已知洗衣机的排水速度为每分钟19升,
① 如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量。
②求排水时y与x之间的函数关系式,并写出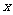 的取值范围.
的取值范围.
22. 如图,AB是圆O的直径,C是AB延长线上一点,CD切圆O于D,过点B作圆O的切线交CD于E,己知∠CDB=∠CAD,AB=CD=2,
如图,AB是圆O的直径,C是AB延长线上一点,CD切圆O于D,过点B作圆O的切线交CD于E,己知∠CDB=∠CAD,AB=CD=2,
(1)△CDB∽△CAD吗?请说明理由,
(2)求CB的长,
(3)求CB的长(选作不计入总分);
23,不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为.
(1)试求袋中蓝球的个数.
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图法,求两次摸到都是白球的概率.
21.某市为了解市民对已闭幕的某一博览会的总体印象,利用最新引进的“计算机辅助电话访问系统”(简称CATI系统),采取电脑随机抽样的方式,对本市年龄在16-65岁之间的居民,进行了400个电话抽样调查.并根据每个年龄段的抽查人数和该年龄段对博览会总体印象感到满意的人数绘制了下面的图(1)和图(2)(部分)
|


|
根据上图提供的信息回答下列问题:
(1)被抽查的居民中,人数最多的年龄段是 岁;
(2)已知被抽查的400人中有83%的人对博览会总体印象感到满意,请你求出31-40岁年龄段的满意人数,并补全图2;
注:某年龄段的满意率=该年龄段满意人数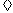 该年龄段被抽查人数
该年龄段被抽查人数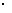 100%.
100%.
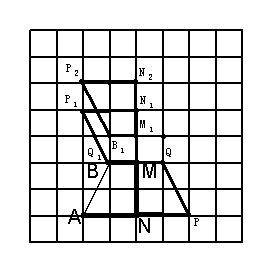
20. 如图,梯形ANMB是直角梯形,
如图,梯形ANMB是直角梯形,
(1)请在图上拼上一个直角梯形MNPQ,使它与梯形ANMB构成一个
等腰梯形.
(2)将补上的直角梯形MNPQ以点M为旋转中心,逆时针旋转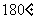 得
得
梯形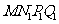 ,(不要求写作法,但要保留作图痕迹)
,(不要求写作法,但要保留作图痕迹)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com