
21.证明:(1)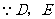 分别为
分别为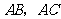 的中点,
的中点, 为中位线.
为中位线.

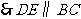 ,且
,且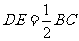 ;
;
又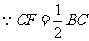 ,
,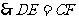 .
.
(2)连结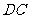 .由(1)可得
.由(1)可得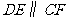 ,且
,且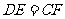 ,
,
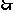 四边形
四边形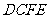 为平行四边形,
为平行四边形,
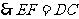 .
.
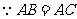 ,且
,且 为中位线,
为中位线,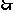 四边形
四边形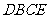 为等腰梯形,
为等腰梯形,
又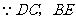 为等腰梯形
为等腰梯形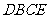 的对角线,
的对角线,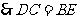 ,
,
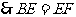 .
.
20.解:(1)设经过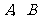 两点的一次函数表达式为
两点的一次函数表达式为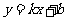 ,
,
则有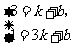
解得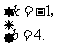
故经过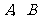 两点的一次函数表达式为
两点的一次函数表达式为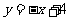 .
.
(2)函数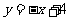 有如下等性质,.
有如下等性质,.
①函数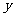 的值随
的值随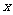 的增大而减小;②函数的图象与
的增大而减小;②函数的图象与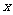 轴的交点为
轴的交点为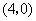 ;
;
③函数的图象与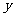 轴的交点为
轴的交点为 ;④函数的图象经过第一、二、四象限;
;④函数的图象经过第一、二、四象限;
⑤函数的图象与坐标轴围成一等腰直角三角形.
(说明:用反比例函数或二次函数解答,同样给分)
19.(1)证明:在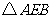 与
与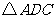 中,
中,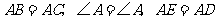 ,
,
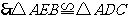 ,
,
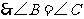 .
.
(2)解:先将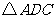 绕点
绕点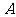 逆时针旋转
逆时针旋转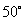 ,再将
,再将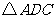 沿
沿
直线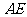 对折,即可得
对折,即可得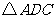 与
与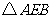 重合.
重合.
 或先将
或先将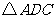 绕点
绕点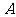 顺时针旋转
顺时针旋转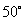 ,再将
,再将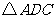 沿直线
沿直线 对折,即可得
对折,即可得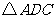 与
与 重合.
重合.
18.解;依题意,可得山高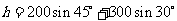
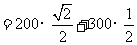
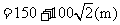
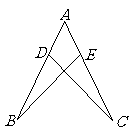 所以山高为
所以山高为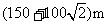 .
.
17.解:(1)“摸出的球是白球”是不可能事件,它的概率为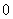 ;
;
(2)“摸出的球是黄球”是不确定事件,它的概率为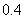 ;
;
(3)“摸出的球是红球或黄球”是必然事件,它的概率为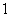 .
.
16.解:解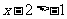 ,得
,得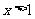 ;
;
解 ,得
,得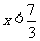 ;
;
所以,原不等式组的解集是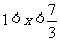 .
.
24.依法纳税是每个公民应尽的义务.《中华人民共和国个人所得税法》规定,公民每月收入不超过1600元,不需交税;超过1600元的部分为全月应纳税所得额,都应纳税,且根据超过部分的多少按不同的税率纳税,详细的税率如下表:
|
级别 |
全月应纳税所得额 |
税率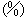 |
|
1 |
不超过500元的 |
5 |
|
2 |
超过500元至2
000元的部分 |
10 |
|
3 |
超过2 000元至5
000元的部分 |
15 |
|
… |
… |
… |
(1)某工厂一名工人2006年5月的收入为2 000元,问他应交税款多少元?
(2)设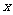 表示公民每月收入(单位:元),
表示公民每月收入(单位:元),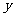 表示应交税款(单位:元),当
表示应交税款(单位:元),当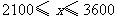 时,请写出
时,请写出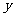 关于
关于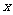 的函数关系式;
的函数关系式;
(3)某公司一名职员2006年5月应交税款120元,问该月他的收入是多少元?
25,如图,已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,E为BC边上的中点,连结DE.
(1) 如图所示,观察猜想DE是⊙O的切线吗?并证明你的结论;
(2) 连结OE、AE,当∠CAB为何值时,四边形AOED是平行四边形,并说明理由.

茂名市第十中学中考综合训练数学试卷(五)
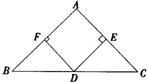
22.已知:如图,D是ΔABC的BC边上的中点,DE⊥AC,DF⊥AB,垂足分别是E、F,且BF=CE.
(1)求证:ΔABC是等腰三角形;
(2)当∠A=900时,试判断四边形AFDE是怎样的四边形,证明你的结论.
23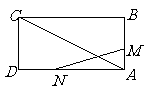 如图,已知矩形
如图,已知矩形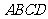 的边长
的边长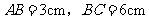 .某一时刻,动点
.某一时刻,动点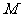 从
从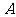 点出发沿
点出发沿 方向以
方向以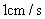 的速度向
的速度向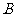 点匀速运动;同时,动点
点匀速运动;同时,动点 从
从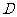 点出发沿
点出发沿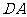 方向以
方向以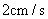 的速度向
的速度向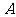 点匀速运动,问:
点匀速运动,问:
(1)经过多少时间,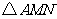 的面积等于矩形
的面积等于矩形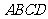 面积的
面积的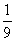 ?
?
(2)是否存在时刻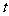 ,使以
,使以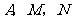 为顶点的三角形与
为顶点的三角形与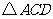
相似?若存在,求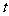 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
21.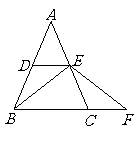 如图,在
如图,在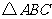 中,
中,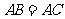 ,点
,点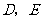 分别是
分别是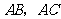 的中点,
的中点,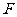 是
是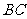 延长线上的一点,且
延长线上的一点,且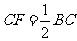 .
.
(1)求证: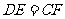 ;
;
(2)求证: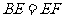 .
.
20.如图,已知点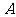 的坐标为
的坐标为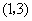 ,点
,点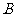 的坐标为
的坐标为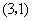 .
.
(1)写出一个图象经过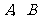 两点的函数表达式;
两点的函数表达式;
(2)指出该函数的两个性质.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com