
05.函数y=(2m-1)x是正比例函数,且y随自变量x的增大而增大,则m的取值范围是
A、m>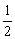 B、m<
B、m<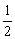 C、m≥
C、m≥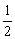 D、m≤
D、m≤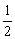
04.下列四个命题中,假命题的是.
A、有三个角是直角的四边形是矩形; B、对角线互相垂直平分且相等的四边形是正方形;
C、四条边都相等的四边形是菱形; D、顺次连接一个四边形各边中点,得到一个菱形,那么这个四边形是等腰梯形.
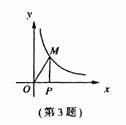
03.反比例函数y= (k>0)在第一象限内的图象如图,点M是图象上点,
MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是
(k>0)在第一象限内的图象如图,点M是图象上点,
MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是
A、 1 B、 2 C、 4 D、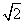
02.张华同学的身高为1.6米,某一时刻他在阳光下的影长为2米,同时与他邻近的一棵树的影长为6米,则这棵树的高为
 A、3.2米 B、4.8米 C、5.2米 D、5.6米
A、3.2米 B、4.8米 C、5.2米 D、5.6米
01.已知x=-1是方程x2+mx+1=0的一个实数根,则m的值是
A、0 B、1 C、2 D、-2
23.解:(1)设蓝球个数为x个
则由题意得= 解得 x=1,即蓝球有1个
(2)树状图或列表正确
两次摸到都是白球的概率 = =
24
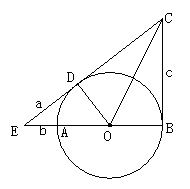 (1)证明:∵CD、CB是⊙O的切线,
(1)证明:∵CD、CB是⊙O的切线,
∴∠ODC=∠OBC=90°
又∵ OD=OB,OC=OC,
∴△OBC≌△ODC(HL)
(2)选择a、b、c,或其中2个均给分;
方法一:在Rt△EBC中,由勾股定理:
(b+2r)2+c2=(a+c)2,得r=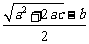 .
.
方法二:Rt△ODE∽Rt△CBE,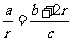 ,得r=
,得r=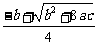 .
.
方法三:连结AD,可证:AD//OC,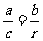 ,得r=
,得r=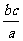 .
.
若选择a、c:需综合运用以上的多种方法,得r=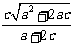 .
.
若选择b、c,则有关系式2r3+br2-bc2=0.
(以上解法仅供参考,只要解法正确均给分)
25,解:(1) 正方形OABC中,因为ED⊥OD,即∠ODE =90°
所以∠CDO+∠EDB=90°,即∠COD=90°-∠CDO,而 ∠EDB =90°-∠CDO,
所以∠COD =∠EDB 又因为∠OCD=∠DBE=90°
所以△CDO∽△BED,
所以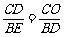 ,即
,即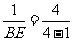 ,得BE=
,得BE=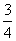 ,
,
则: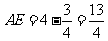
因此点E的坐标为(4,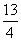 ).
).
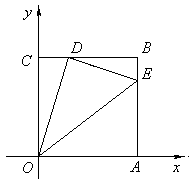 (2) 存在S的最大值.
(2) 存在S的最大值.
由△CDO∽△BED,
所以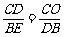 ,即
,即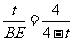 ,BE=t-
,BE=t-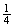 t2,
t2,
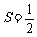 ×4×(4+t-
×4×(4+t-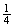 t2)
t2) .
.
故当t=2时,S有最大值10.
16. 解:原式= 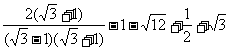
= 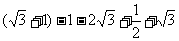 =
= 
17,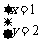
18,因为 B=
比较可知,A与B只是分式本身的符号不同,所以A、B互为相反数.
19, 解:(1)∠ABC=135°, BC=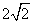 ;
;
(2)能判断△ABC与△DEF相似(或△ABC∽△DEF)
这是因为∠ABC =∠DEF = 90°+45°=135° , 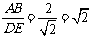 ,
,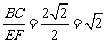
∴ 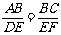 ∴△ABC∽△DEF.
∴△ABC∽△DEF.
20,
(1) 解:y=5000+20x
(2) 解法1:设公司至少要售出x套产品才能确保不亏本,则有:
70 x≥5000+20x 解得:x≥100
解法2:每套成本是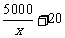 若每套成本和销售价相等则:
若每套成本和销售价相等则: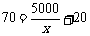
解得: x=100 因此公司至少要售出100套产品才能确保不亏本
11.> 12.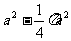 13.150×80%-x=20%x 14.①、③、⑤ 15、
13.150×80%-x=20%x 14.①、③、⑤ 15、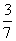 ;
;
BCDCB ACC CA
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com