
2.用配方法解方程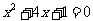 ,经过配方,得到( )
,经过配方,得到( )
A.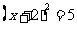 B.
B.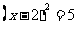 C.
C.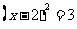 D.
D.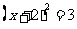
1.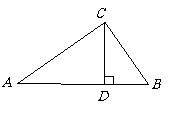 如图,在
如图,在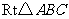 中,
中,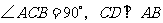 于点
于点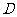 .
.
已知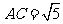 ,
,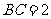 ,那么
,那么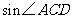 =( )
=( )
A.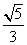 B.
B.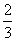 C.
C.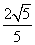 D.
D.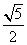
5.关注学生的能力培养,重视试题的创新
(1)重视实际背景的创新
 例16
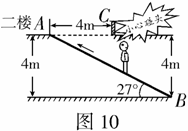
(2008长沙)如图10所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,请你根据图中数据计算回答:小敏身高1.78米,她乘电梯会有碰头危险吗?姚明身高2.29米,他乘电梯会有碰头危险吗?(可能用到的参考数值:
例16
(2008长沙)如图10所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,请你根据图中数据计算回答:小敏身高1.78米,她乘电梯会有碰头危险吗?姚明身高2.29米,他乘电梯会有碰头危险吗?(可能用到的参考数值: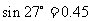 ,
,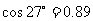 ,
,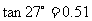 )
)
点评:解决这道题所运用的数学知识并不复杂,从创新的角度来看,该题选择了学生司空见惯的超市背景以及所熟知的体育明星姚明,从而使问题给人以耳目一新之感.
例17
(2008益阳)如图11,矩形纸片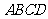 中,
中, ,
,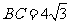 ,将矩形沿对角线
,将矩形沿对角线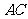 剪开,解答以下问题:
剪开,解答以下问题:
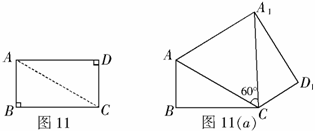
(1)将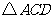 绕点
绕点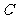 顺时针旋转
顺时针旋转 ,
,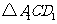 是旋转后的新位置(图11(
是旋转后的新位置(图11(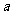 )),求此时
)),求此时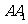 的距离;
的距离;
(2)将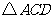 沿对角线
沿对角线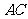 向下翻折(点
向下翻折(点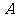 ,点
,点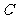 位置不动,
位置不动,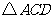 和
和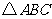 落在同一平面内),
落在同一平面内), 是翻折后的新位置(图11(
是翻折后的新位置(图11(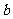 )),求此时
)),求此时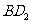 的距离.
的距离.
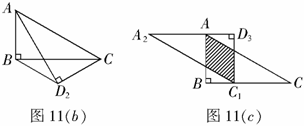
(3)将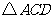 沿
沿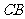 向左平移,设平移的距离为
向左平移,设平移的距离为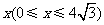 ,
,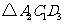 是平移后的新位置(图11(
是平移后的新位置(图11(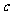 )),若
)),若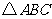 与
与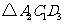 重叠部分的面积为
重叠部分的面积为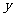 ,求
,求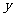 关于
关于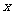 的函数关系式.
的函数关系式.
点评:本题考查同学们运用旋转、平移、翻折的性质,结合直角三角形和全等三角形的有关知识,全面寻找图形旋转、平移、翻折过程中的不变量.为了降低难度,题目从易到难,层层递进,这样的设计符合中考题的特点,使整套试卷的梯度更加明显,有利于学生的正常发挥.
(2)重视问题情境的创新
例18 (2008衡阳)国家为了关心广大农民群众,增强农民抵御大病风险的能力,积极推行农村医疗保险制度,某县根据本地的实际情况,制定了纳入医疗保险的农民医疗费用报销规定.享受医保的农民可在定点医院就医,在规定的药品品种范围内用药,由患者先垫付医疗费用,年终到医保中心报销,医疗费的报销比例标准如下表:
|
费用范围 |
500元以下 (含500元) |
超过500元且不超 过1000元的部分 |
超过10000 元的部分 |
|
报销比例标准 |
不予报销 |
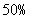 |
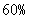 |
(1)设刘爷爷一年的实际医疗费为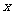 元(
元(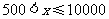 ),按标准报销的金额为
),按标准报销的金额为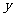 元,试求
元,试求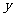 与
与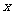 的函数关系式.
的函数关系式.
(2)若刘爷爷一年内自付医疗费为2000元(自付医疗费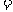 实际医疗费
实际医疗费 按标准报销的金额),则刘爷爷当年实际医疗费为多少元?
按标准报销的金额),则刘爷爷当年实际医疗费为多少元?
(3)若刘爷爷一年内自付医疗费不小于6250元,则刘爷爷当年实际医疗费至少为多少元?
例19
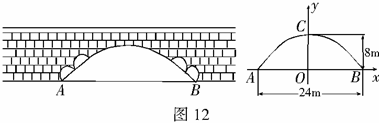
(2008永州)如图12所示是永州八景之一的愚溪桥,桥身横跨愚溪,面临潇水,桥下冬暖夏凉,常有渔船停泊桥下避晒纳凉.已知主桥拱为抛物线型,在正常水位下测得主拱宽24m,最高点离水面8m,以水平线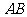 为
为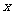 轴,
轴,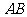 的中点为原点建立坐标系.
的中点为原点建立坐标系.
(1)求此桥拱线所在抛物线的解析式.
(2)桥边有一浮在水面部分高4m,最宽处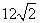 m的河鱼餐船,试探索此船能否开到桥下?说明理由.
m的河鱼餐船,试探索此船能否开到桥下?说明理由.
例20 (2008长沙)某班到毕业时共结余经费1800元,班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品,其余资金用于在毕业晚会上给50位同学每人购买一件文化衫或一本相册作为纪念品.已知每件文件衫比每本相册贵9元,用200元恰好可以买到2件文化衫和5本相册.
(1)求每件文化衫和每本相册的价格分别为多少元?
(2)有几种购买文化衫和相册的方案?哪种方案用于购买老师纪念品的资金更充足?
点评:以上三道例题,充分体现数学源于生活,又服务于生活,以同学们身边的事例为背景,体现了试卷的公平性.
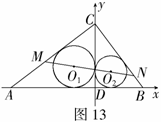 例21 (2008株州)已知
例21 (2008株州)已知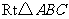 ,
,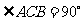 ,
, ,
,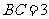 ,
,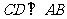 于点
于点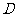 ,以
,以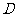 为坐标原点,
为坐标原点,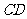 为在直线为
为在直线为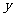 轴建立如图13所示平面直角坐标系.
轴建立如图13所示平面直角坐标系.
(1)求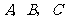 三点的坐标;
三点的坐标;
(2)若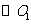 ,
, 分别为
分别为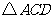 ,
,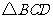 的内切圆,求直线
的内切圆,求直线 的解析式;
的解析式;
(3)若直线 分别交
分别交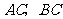 于点
于点 ,判断
,判断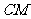 与
与 的大小关系,并证明你的结论.
的大小关系,并证明你的结论.
点评:本题有多种解法,重视解法多样化,实际上就是给不同的学生以不同的选择,即让不同的人在数学上有不同的发展.
总之,湖南省各地州市2007年的命题,能够承前启后,继往开来,在把握数学新课程导向的基础上,既注重命题的发展和创新,同时又能充分发挥试题的教育功能,全面关注学生的数学基础和能力,从而不断地将数学新课程扎扎实实向纵深方向又快又好地推进.
4.内涵丰富,较好地体现了数学的价值观.很多试卷内涵较为丰富,知识、技能、思想方法,数学思考与数学活动,解决问题的能力等方面展现得较为充实,并具有一定的层次性.
(1)重点考查学生
例13
(2008娄底)经过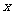 轴上
轴上 两点的抛物线
两点的抛物线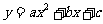 交
交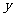 轴于点
轴于点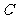 ,设抛物线的顶点为
,设抛物线的顶点为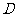 ,若以
,若以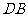 为直径的
为直径的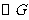 经过点
经过点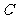 ,求解下列问题:
,求解下列问题:
(1)用含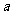 的代数式表示出
的代数式表示出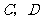 的坐标;
的坐标;
(2)求抛物线的解析式;
(3)如图8,当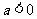 时,能否在抛物线上找到一点
时,能否在抛物线上找到一点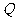 ,使
,使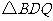 为直角三角形?你能写出
为直角三角形?你能写出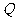 点的坐标吗?
点的坐标吗?
点评:本题将二次函数、平面直角坐标系,圆的知识结合在一起考查,有效地考查了学生综合运用数学知识分析问题、解决问题的能力.也是在中考复习中师生应着力培养的一种数学素养.
 例14
(2007娄底)去年夏季山洪暴发,我市好几所学校被山体滑坡推倒教学楼,为防止滑坡,经过地质人员勘测,当坡角不超过
例14
(2007娄底)去年夏季山洪暴发,我市好几所学校被山体滑坡推倒教学楼,为防止滑坡,经过地质人员勘测,当坡角不超过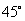 时,可以确保山体不滑坡.某小学紧挨一座山坡,如图9所示,已知
时,可以确保山体不滑坡.某小学紧挨一座山坡,如图9所示,已知 ,斜坡
,斜坡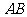 长30米,坡角
长30米,坡角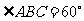 .改造后斜坡
.改造后斜坡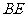 与地面成
与地面成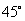 角,求
角,求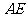 至少是多少米?(精确到0.1米)
至少是多少米?(精确到0.1米)
点评:这个题目实质是考查如何计算竖直物体的高度,但所提问题却是如何解决实际问题,所考查的解决问题策略均是“转化”(转化为解直角三角形).这样的考法体现了数学的价值和作用,具有较好的效度和可推广性,对深入实施教学改革具有积极的推动作用.学数学,用数学,是新课程的显著特点.
(2)设置与生活和社会实际相关的问题考查运用方程解决简单实际问题的能力.
例15
(2008怀化)2007年我市某县筹备20周年县庆,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配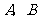 两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个
两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个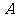 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个
种造型需甲种花卉80盆,乙种花卉40盆,搭配一个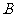 种造型需甲种花卉50盆,乙种花卉90盆.
种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个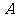 种造型的成本是800元,搭配一个
种造型的成本是800元,搭配一个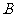 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
点评:这个问题解答严格遵循“实际问题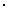 数学问题
数学问题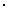 解数学问题
解数学问题 解决实际问题”,对于考查“数学化”(如列方程、列不等式、列方程组、列不等式组等)具有较高的效度.本题在一定程度上考查了学生在生活中用数学的意识,本题有利于提高试卷的效度和信度.
解决实际问题”,对于考查“数学化”(如列方程、列不等式、列方程组、列不等式组等)具有较高的效度.本题在一定程度上考查了学生在生活中用数学的意识,本题有利于提高试卷的效度和信度.
3.注意整体结构的相互联系和层次性.试卷注重整体结构的相互联系和层次性,在设计试题时,能注重前后问题的联系性和层次性,前面的小问题往往为解决后面较复杂的问题作铺垫,提供解题思路或解决后面问题的数据资料.
(1)考查探究与推理,注重联系与综合
例10
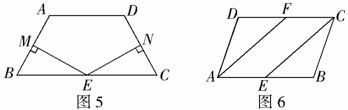
(2008郴州)如图5
,在等腰梯形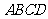 中,
中,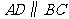 ,
,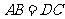 ,点
,点 是
是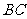 边的中点,
边的中点,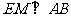 ,
,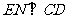 ,垂足分别为
,垂足分别为 .求证:
.求证: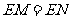 .
.
点评:将等腰梯形与三角形的知识结合在一起,需要学生充分了解二者的区别和联系,同时还要从图形的变化、变换,灵活运用相关性质解题.
(2)注重利用三角形全等知识考查学生的推理判断能力
例11
(2008永州)如图6,在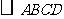 中,点
中,点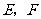 分别在
分别在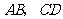 上,连结
上,连结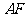 、
、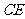 .请添加一个你认为合适的条件
,使
.请添加一个你认为合适的条件
,使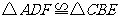 ,并给予证明.
,并给予证明.
点评:本例是一道开放性问题,在作答不确定的情况下考查学生对三角形全等知识的掌握.是近几年对开放性问题比较经典的考法.
(3)注重利用切线的判定和性质,综合考查学生的各种能力
例12
(2008衡阳)如图7,点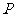 在
在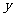 轴上,
轴上,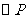 交
交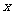 轴于
轴于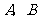 两点,连结
两点,连结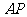 并延长交
并延长交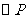 于
于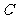 点,过点
点,过点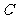 的直线
的直线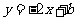 交
交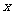 轴于点
轴于点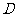 ,交
,交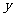 轴于点
轴于点 ,且
,且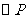 的半径为
的半径为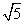 ,
, .
.
(1)求点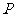 ,点
,点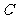 的坐标;
的坐标;
(2)求证: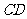 是
是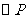 的切线;
的切线;
(3)若二次函数 的图象经过
的图象经过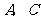 两点,求这个二次函数的解析式,并写出使函数值大于一次函数
两点,求这个二次函数的解析式,并写出使函数值大于一次函数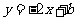 值的
值的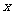 的取值范围.
的取值范围.
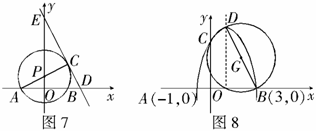
2.通过操作实验,自己探究,考查数学思维能力和分析、解决问题的能力.试题注重考查同学们的动手操作及实验探究的能力,考查同学们运用数学思想方法,分析问题和解决问题的能力.
(1)以平移、旋转条件下的探究性问题考查探究能力
例8 (2008岳阳)如图3,在一个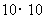 的正方形
的正方形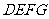 网格中有一个
网格中有一个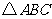 .
.
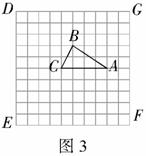
(1)在网格中画出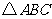 向下平移3个单位得到的
向下平移3个单位得到的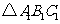 ;
;
(2)在网格中画出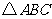 绕
绕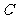 点逆时针方向旋转
点逆时针方向旋转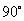 得到的
得到的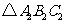 ;
;
(3)若以 所在直线为
所在直线为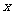 轴,
轴,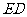 所在的直线为
所在的直线为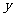 轴建立直角坐标系,写出
轴建立直角坐标系,写出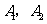 两点的坐标.
两点的坐标.
点评:这两题将平移与旋转有机的结合起来,考查同学们能按照要求作出简单平面图形旋转后的图形,在一定程度上也考查同学们切实理解运动变换及数形结合的思想方法.
(2)利用几何体的视图与投影、平面图形的分解与组合考查空间观念.
例9 (2008湘潭)从左面观察图4所示机器零件,看到的是( )
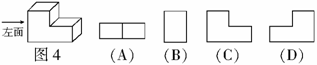
点评:几何体的视图展开与折叠,是培养学生空间想象能力的好素材.本题运用几何体的视图,较好体现了“观察--思考--猜测--验证”这一课标所提出的要求,同时也考查了学生的空间观念.
1.体现数学的基础性与普及性,注重数学与生活和社会的联系,重视应用能力.试题注重考查初中数学的核心内容,注重数学与生活、社会和其它学科的联系,激发同学们学习数学的兴趣,有利于引导初中数学教学加强同学们的应用意识的培养.
(1)重视对基础知识和基本概念的考查.
例1 (2008常德)据科学家测算,用1吨废纸造出的再生好纸相当于0.3~0.4亩森林木材的造纸量.我市今年大约有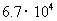 名初中毕业生,每个毕业生离校时大约有12公斤废纸,若他们都把废纸送到回收站生产再生好纸,则至少可使森林免遭砍伐的亩数为_____亩.
名初中毕业生,每个毕业生离校时大约有12公斤废纸,若他们都把废纸送到回收站生产再生好纸,则至少可使森林免遭砍伐的亩数为_____亩.
点评:对基础概念的考查一方面有利于了解考生数学知识的基本功底,另一方面有利于引导教师的教学,同时对面向全体同学,落实课程标准的相关目标,将产生深刻的影响.
(2)重视对基本运算能力的考查
例2 (2008长沙)计算: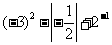 .
.
点评:《课程标准》所规定的基本的运算能力应当是同学们必须具备的,各地的考题均控制在标准所要求的难度之内.同时对简单的负指数幂、零指数幂的考查以及结合特殊角的三角函数值进行混合运算受到各地命题人的青睐.
(3)重视在实际背景考查数学知识和能力
例3 (2008郴州)根据天气预报,明天的降水概率为15%,后天的降水概率为70%,假如小明准备明天或者后天去放风筝,你建议他_________天去为好.
点评:本题选择了天气预报这一常识性问题,考查了同学们对概率本质的把握情况,在重视基本的核心内容的基础上,又加强了数学与社会生活实际的联系.
例4 (2008怀化)2008年8月第29届奥运会在北京开幕,5个城市的国际标准时间(单位:时)在数轴上表示如图1所示,那么北京时间2008年8月8日20时应是( )
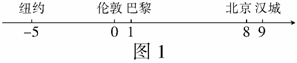
(A)伦敦时间2008年8月8日11时
(B)巴黎时间2008年8月8日13时
(C)纽约时间2008年8月8日5时
(D)汉城时间2008年8月8日19时
点评:以奥运会为背景材料,结合数轴及相关的地理知识,跨学科、多角度考查同学们对基础数学知识和思想方法的了解.是一道值得借鉴的试题.
例5 (2008永州)永州市内货摩(运货的摩托)的运输价格为:2千米内运费5元;路程超过2千米的,每超过1千米增加运费1元,那么运费y元与运输路程x千米的函数图象是( )

点评:本题以实际生活为背景,在加强对一次函数图象的识图能力和分析问题能力考查的同时,也引导同学们平时关注生活中蕴含的数学问题.这样的题目,既突出了函数的基础性功能,又突出了它的应用性功能,对改进和完善中考数学命题具有积极的启示作用.
例6 (2007邵阳)2007年上半年,全国猪肉价格持续上涨.针对这种现象,我市某校数学课外兴趣小组的同学对当地上半年猪肉价格和小明一家对肉类食品的消费情况进行了调查,并将收集的数据进行分析整理,绘制了统计图表,如图2.请结合图表,回答下列问题.
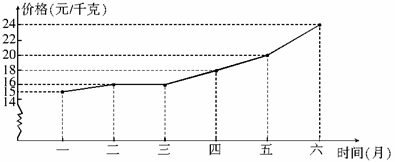
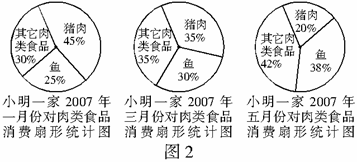
(1)试求2007年1-6月份猪肉价格的极差;
(2)若小明一家每月对肉类食品的消费金额为200元,则小明一家一月份、三月份、五月份的猪肉消费金额分别为多少元;
(3)根据所求数据,并结合统计图表,你能获得什么信息.
点评:选取社会敏感的与生活息息相关的材料命制试题,既体现了命题人的社会责任感,同时对同学们的数学素养也是一种很好的考查.
例7 (2008怀化)“六一”儿童节前夕,我市某县“关心下一代工作委员会”决定对品学兼优的“留守儿童”进行表彰,某校八年级8个班中只能选两个班级参加这项活动,且8(1)班必须参加,另外再从其他班级中选一个班参加活动.8(5)班有同学们建议采用如下的方法:将一个带着指针的圆形转盘分成面积相等的4个扇形,并在每个扇形上分别标上1,2,3,4四个数字,转动转盘两次,将两次指针所指的数字相加,(当指针指在某一条等分线上时视为无效,重新转动)和为几就选哪个班参加,你认为这种方法公平吗?请说明理由.
点评:将概率知识中的两种求概率的基本方法---列表法、画树状图法置于一个贴近同学们生活实际背景的材料中考查,不仅提高了试题的信度和效度,而且凸现了数学考试的人文价值.
(三)全省学业考试数学试卷试题的命题特点
1.寻求两考平衡,凸显学业考试特征
各地数学试题严格按照《数学课程标准》和《考试标准》的要求命制,同时充分考虑本地区的初中数学教育教学实际,在升学选拔与毕业水平考试中寻求平衡点,但更突出试卷的学业考试特征.
2.注重基础考查,突出核心内容重点考查
各地数学试题注重对初中阶段同学们必须掌握的基础知识、基本技能、基本数学思想和数学方法的考查,特别是初中数学领域的核心内容,如函数、方程、不等式等,也是同学们后续学习的必备知识,大多数试卷能够从不同角度设计试题进行全方位的重点考查.
3.创设生活情景,关注数学人文价值
各地试题均能较好地关注同学们的生活实际,在同学们熟悉的情境中命制试题,同时在试卷中关注数学的人文价值.许多地方的试题均能选取同学们身边的数学问题,体现了公平的原则,让同学们体会到数学既来源于生活又服务于生活.
4.命制创新试题,考查综合实践能力
各地遵循新课程理念,命制了一些创新试题,注重对同学们实践能力与创新能力的考查.
(二)学业考试数学试卷的知识结构
数与代数、空间与图形和统计与概率所占的百分比将完全按《考试标准》的要求进行,试题按其难度分为容易题、稍难题和较难题、难度控制在0.65-0.8范围内.
(一)学业考试数学试卷的呈现方式
各地的中考命题在《数学课程标准》和《考试标准》的指导下,在呈现方式上存在如下一些特点.
1.在要求上:2004-2007年湖南省各地的数学试卷均采用了闭卷笔试形式,在分值上主要有满分100分和120分两种,考试时间均为120分.
2.在题型上:试题分为选择题、填空题和解答题三种题型,各类题型均按《考试标准》的要求进行设置.以长沙市为例,第一大题为填空题,共8道小题,每小题3分,满分24分;第二大题为选择题,共8道小题,每小题3分,满分24分;第三大题为解答题,每小题6分,满分36分;第四大题为解答题,每小题8分,满分16分;第五大题为解答题,共两道小题,每小题10分,满分20分.试题的数量和难度各地均控制在“省标”的要求之内,应当说均很好地把握了数学新课程的导向.师生在复习迎考时应当着重把握《数学课程标准》和《考试标准》的精神.
3.在形式上:各地的试卷一改以往的单调、呆板、枯燥的面孔,增加了各种帮助同学们理解的情境和场景,有利于考试时更好地理解试卷和试题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com