
(3)设抛物线的焦点为F,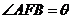 ,试问
,试问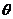 角能否等于120°?若能,求出相应的直线l的方程;若不能,请说明理由.
角能否等于120°?若能,求出相应的直线l的方程;若不能,请说明理由.
(2)若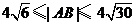 ,求直线l的斜率k的取值范围;
,求直线l的斜率k的取值范围;
直线l与抛物线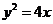 交于两点A、B,O为坐标原点,且
交于两点A、B,O为坐标原点,且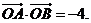
(1)求证:直线l恒过一定点;
21.(本小题满分14分)
(3)令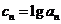 ,判断在数列{cn}中是否存在某连续的三项或三项以上的项,按原来的排列顺序得到的数列是等比数列?为什么?
,判断在数列{cn}中是否存在某连续的三项或三项以上的项,按原来的排列顺序得到的数列是等比数列?为什么?
已知数列{an}为等差数列,a1=2,且该数列的前10项和为65,若正数列{bn}满足条件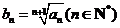 .
.
(1)求数列{bn}的通项公式;
(2)求数列{bn}的最大项;
20.(本小题满分13分)
已知二次函数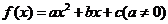 和一次函数
和一次函数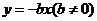 ,其中a、b、c满足条件a>b>c,且a+b+c=0;
,其中a、b、c满足条件a>b>c,且a+b+c=0;
(1)证明:一次函数与二次函数的图象必有两个不同交点A、B;
(2)求线段AB在x轴上的射影A1B1的长的取值范围.
19.(本小题满分12分)
排球比赛的规则是5局3胜制,已知每局比赛中甲、乙两队获胜的概率分别为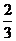 、
、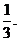
(1)若前两局中乙队以2∶0领先,求最后甲、乙队各自获胜的概率;
(2)乙队以3∶2获胜的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com