
(3)若数列 满足
满足 ,
, 是数列
是数列 前
前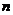 项的和,是否存在正实数
项的和,是否存在正实数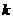 ,使不等式
,使不等式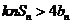 对于一切的
对于一切的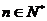 恒成立?若存在指出
恒成立?若存在指出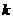 的取值范围,并证明;若不存在说明理由.
的取值范围,并证明;若不存在说明理由.
(2)若数列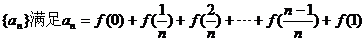
 ,求数列
,求数列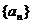 的通项公式;
的通项公式;
(1)求 的值;
的值;
20.已知函数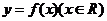 满足
满足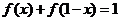 .
.
 (2)要使公园所占面积最小,休闲区
(2)要使公园所占面积最小,休闲区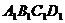 的长和宽该如何设计?
的长和宽该如何设计?
(1)若设休闲区的长和宽的比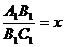 ,求公园
,求公园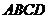 所占面积
所占面积 关于
关于 的函数
的函数 的解析式;
的解析式;
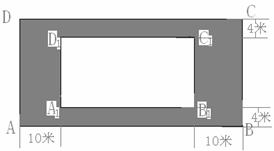
19.某房地产开发公司计划在一楼区内建造一个长方形公园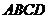 ,公园由长方形的休闲区
,公园由长方形的休闲区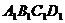 和环公园人行道(阴影部分)组成.已知休闲区
和环公园人行道(阴影部分)组成.已知休闲区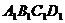 的面积为
的面积为 平方米,人行道的宽分别为
平方米,人行道的宽分别为 米和
米和 米(如图)
米(如图)
(2) 判断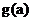 的单调性, 并求出
的单调性, 并求出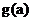 的最小值.
的最小值.
(1)
求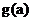 的函数表达式;
的函数表达式;
 , 令
, 令 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com