已知数列 和满足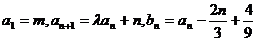

（Ⅱ）若直线 与双曲线 G相交于P、Q两点(不重合于左、右顶点)，且以PQ为直径的圆过双曲线G的右顶点D．求证：直线过定点'并求出该点的坐标

(22)(本小题满分12分)

    已知离心率为 的双曲线G的中心在坐标原点，左、右焦点F₁、F₂在x 轴上，双曲线G的右支上一点A使 且△F₁AF₂的面积为l

    ( I )求双曲线G的标准方程，

    (Ⅱ)是否存在实数k，使方程喜 有四个不同的实根?若存在，求出k的取值范厨；若不存在，请说明理由．

(21)(本小题满分12分)

    (I)若 l，求证：

   已知函数  

    在斜三棱柱ABC―A₁B₁C₁中，已知侧面A₁ACC₁⊥底面ABC底面 ABC是边长为2的正三角形，A₁A=A₁C，A_lA⊥A₁C．    -

(I)求证：A₁C₁⊥B₁C

(Ⅱ)求二面角B₁―A₁C―C₁的大小

 (20)(本小题满分12分)

标中的第四项不合格或其它三项指标中有两项不合格，则这种品牌的食品不能上市．已知每项检测是相互独立的，第四项指标抽检出现不合格的概率是，且其它三项指标抽检出现不合格的概率均是?

    (I)若食品监管部门要对其四项质量指标依次进行严格的检测，求恰好在第三项指标检

测结束时，能确定该食品不能上市的概率；

    (1I)求该品牌的食品能上市的概率．

（19)(本小题满分12分)

(Ⅱ)若 ，求的值．

(18)(本小题满分12分)

    食品监管部门要对某品牌食品四项质量指标在进入市场前进行严格的检测．如果匹项指

(I)求的最小正周期及函数图象的对称中心