2.棱长2厘米的正方体表面积与体积比是多少?把它放入红墨水里，它6面共24平方厘米被染红，我用刀把它切成4个棱长1厘米的小正方体，每个小正方体有几面被染红?面积是多少?面积与体积比又是多少?

1.把棱长1厘米的正方体放入红墨水里，有几面被染红?面积是多少?面积与体积比是多少?

2.多细胞生物通过细胞分裂产生生殖细胞而繁殖后代；通过细胞分裂使生物体内细胞数目增多，从而使新个体由小长大，使生物体不断更新衰老死亡的细胞，从而保证生物体的正常生命活动。

[教学反思]

　在经过最初两个班的教学实践后，我发现活动中问题的设计以及组织讨论的效果比较好，大多数学生理解了细胞的体积与表面积(细胞膜)、细胞大小与物质交换的关系，但部分学生搞不清楚其中的关系。后来又做了改进，我自己用马铃薯做了一些棱长为1厘米、2厘米、3厘米的正方体，用红墨水进行演示。又设计了一些问题。

1.单细胞生物通过细胞分裂进行繁殖。

2.植物细胞分裂过程：核分裂―新细胞膜、细胞壁―2个新细胞

　在细胞分裂时，细胞核内会发生什么变化呢?同学们还记得细胞核的作用吗?　 (在遗传有重要作用)为什么细胞核能在遗传中起重要作用呢?

　结合挂图分析讲解染色质、染色体的概念以及在细胞分裂过程中的变化。

　强调染色质里含有遗传物质。细胞分裂前，染色质细长，经过复制而数量倍增，分裂时，染色质缩短变粗变为染色体，并且平均分配到两个子细胞中，从而保证了新细胞与亲代细胞具有相同的遗传物质。因此染色质与染色体是同一种物质在细胞分裂的不同时期的两种表现形式。

　通过学习，同学们分析、讨论一下细胞分裂有什么特点?然后归纳总结。

　细胞通过分裂把染色体(遗传物质)平均分配到两个新细胞中，保证了新细胞与亲代细胞具有相同的遗传物质。

　细胞分裂又有什么意义?

　同学们说得对，我们把一个细胞变为两个细胞的过程称为细胞分裂。细胞是如何从一个变为两个的呢?这是一个非常复杂的过程，同学们先观看动物细胞和植物细胞的分裂过程。(播放课件)　　

讨论动物细胞和植物细胞的分裂过程，再用自己的语言描述细胞分裂过程，归纳、总结。

1.动物细胞分裂过程：核分裂―细胞质分开―2个新细胞

　通过上一节课的学习，我们知道细胞体积很小，而细胞又能不断地生长，那么细胞将怎样才能保持较小的体积呢?生物体内那么多细胞又是怎么来的呢?

　一种方式就是细胞长到一定程度，就停止生长；另一种是细胞长到一定大小的时候，细胞可能一分为二，同学们认为会是哪一种呢?　 (答：第二种)

3.如果把棱长3厘米的正方体放入红墨水里，情况会如何呢?(平均2面，2平方厘米，2／1)

　如果把正方体换为其他的几何模型，结论也是一样的，因此我们也可以把这个结论应用到细胞中去，同学们能说说看吗?

　学生答：细胞越大，细胞膜面积与体积比则越小；细胞越小，细胞膜面积与体积比则越大。

　设问：这对细胞有什么好处或意义呢?　 (激发思考)

　问：体积较大细胞与体积较小细胞比较，在生活中哪种细胞需要从外界环境获取更多的营养物质呢?谁又会产生更多的废物要排出体外呢?

　答：体积较大的细胞。

　问：如果细胞无限生长，同学们讨论一下，看会有什么情况出现?　 (较大细胞的表面积即细胞膜的面积相对较小，细胞膜将不能保证从外界环境获取足够的生活物质供细胞进行生命活动。)

　问：同学们现在理解了细胞为什么这么小吗?

　答：较小细胞的表面积则相对较大，更易于保证细胞与外界进行物质交换，从而保证细胞正常的生命活动。

　　　　　　　　　　　第二课时

2.棱长2厘米的正方体表面积与体积比是多少?(3／1)把它放入红墨水里，它6面共24平方厘米被染红，我用刀把它切成4个棱长1厘米的小正方体，每个小正方体有几面被染红?面积是多少?面积与体积比又是多少?　 (3面，3平方厘米，3/1)

　通过学习我们知道生物体内的活细胞是有生命的(即我们通常所说细胞是活的)。细胞进行生命活动就要通过细胞膜从细胞周围环境中获得营养物质，排出代谢废物，那细胞体积小是否与细胞进行生命活动中的物质交换有关呢?(引导提出探究的问题)　 你们认为呢?　 (激发了学生的兴趣，吸引了他们的注意力，纷纷提出自己的看法或观点)然后师生共同归纳。

　有的同学认为是，有的认为不是。那你们怎样设计实验去证明自己的观点呢?有的学生就小声议论：细胞那么小，又看不到，我们没有那么小的工具来测量细胞大小，用什么方法才能去证明呢?

　同学们议论得好，细胞体积很小，我们很难对细胞的体积和细胞膜的表面积进行精确的测量和计算，就是科学家也很难对细胞进行精确测量，怎么办呢?

　科学家通常是通过建立数学模型来研究某些复杂或不易直接进行研究的问题。针对这个问题，我们可以用较大的正方体模型代替细胞，如用棱长分别为1厘米、2厘米、3厘米、4厘米的正方体，先计算小正方体的表面积和体积，再将两者进行比较，问题就转化为研究正方体的体积和表面积的关系了，这样问题就简化、易于理解了。

　同学们可以拿出课前要求大家准备的正方体进行实验了，但我们先来预测一下结果，四个正方体的体积与表面积的比是随着体积的增大而变大，还是减小呢?

　(学生讨论并进行预测，可能的预测有三种：随着正方体的体积增大，(1)比值增大，(2)比值减小，(3)比值不变。)

　预测后，学生分别计算四个正方体的体积和表面积及比值，并将数据记录在课本上的表格内。

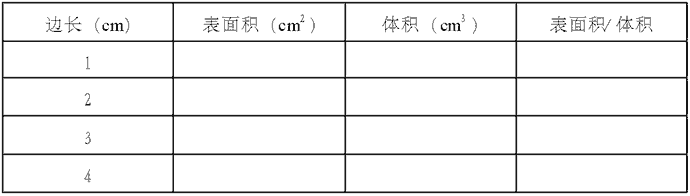
　讨论、分析正方体的体积和表面积比的变化有什么规律，与自己的预测是否相符。

　学生汇报正方体的表面积与体积比。

　从数据可看出，四个正方体从小到大，其表面积和体积的比分别为6、3、2、3／2，如果正方体的体积再增大，比值会怎么样呢?　 (学生答：减小)我们可得出什么结论呢?(学生答：正方体的体积越大，表面积与体积比则越小，反之则越大。)为了让学生都能理解细胞大小与物质交换的关系，再如下提问。

1.把棱长1厘米的正方体放入红墨水里，有几面被染红?面积是多少?表面积与体积比呢?　 (6面，6平方厘米，6／1)