3．画出该配合物(或配离子)的立体结构；4．配合物X是如何形成超分子的

第八题(11分)从昆虫斑蟊体内的可提取得到的一种化合物斑蟊素(A)具有明显的抗肿瘤活性。斑蟊素为酸酐化合物，在体内易于水解，临床对治疗肝癌和膀胱癌有效，但具有泌尿道和消化道副作用。将酸酐与取代胺作用，可生成不同取代基的酰亚胺，水解将慢于酸酐，在体内将逐渐释放斑蟊酸，毒性大大降低。为此，科学家设计合成了羟基斑蟊素(B)

根据以上知识 请回答：

8-1 找出化合物A中的手性碳，并在结构式(见右图)中用“ * ”记号加以标明。

8-2 已知化合物A的优势构象为，则它__________(填“有”或“无”)旋光性。

8-3 根据系统命名法，的名称为____________________________________________。

8-4 提出一条以和为原料(其他原料任选)合理的合成化合物B的路线，写出合成过程，并注明反应条件。

第九题 (8分)利用氢能离不开储氢材料。利用合金储氢的研发，以获得重大进展。研究发现LaNix是一种很好的储氢合金。(相对原子质量：La-138.9)

　LaNix属六方晶系(图c)，晶胞参数a ₀=511pm，c ₀=397pm。储氢位置有两种，分别是八面体空隙 (“■”)和四面体空隙(“▲”)，见图a、b，这些就是氢原子存储处。有氢时，设其化学式为LaNixHy。

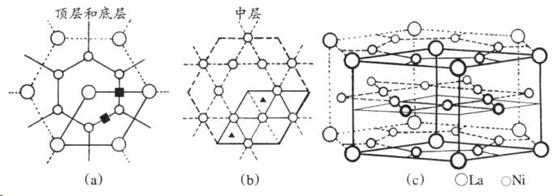
10-1 合金LaNix中x的值为________；晶胞中和“■”同类的八面体空隙有______个，并请在图a中标出；和“▲”同类的四面体空隙有______个，并请在图b中标出。

10-2 若每个八面体空隙中均储有H，LaNixHy中y的值是_______。

10-3 若H进入晶胞后，晶胞的体积不变，H的最大密度是____________ g · cm^-3

第十题 (7分) 同时具备几种功能的多功能材料往往具有特殊的用途而成为材料领域的热点。南京师大结构化学实验室最近设计合成了一种黄色对硝基苯酚水合物多功能晶体材料：

C₆H₅NO₃·1.5H₂O。实验表明，加热至94℃时该晶体能由黄色变成鲜亮的红色，在空气中温度降低又变为黄色，即具有可逆热色性；同时实验还表明它具有使激光倍频的二阶非线性光学性质。X-射线衍射结果表明该晶体属于单斜晶系，晶胞参数a=2119.8 pm，b=367.5 pm，c=1037.6pm，α=γ=90.0°，β=117.2°，密度1.535 g · cm^-3，在晶体中水分子通过氢键把对硝基酚分子连接起来而形成层状结构。

10-1 在上述晶体中形成氢键的氧原子坐标为(0.87，0.88，0.40；0.49，0.91，0.34；0.50，0.42，0.50)，请计算晶体中氢键的键长。

10-2 预期上述晶体材料可以作为掺杂材料的主体，在层间嵌入某种金属离子而形成具有特殊功能的掺杂材料，嵌入离子的密度与材料性质密切相关。假设在晶体中每个苯环通过静电与一个嵌入离子相互作用，试计算每立方厘米上述晶体能嵌入离子的数目。

10-3 热分析试验表明，当温度升高到94℃时该晶体开始失重，到131℃重量不再变化，比原来轻了16.27%。试给出该晶体完全变色后的化学式；并据此分析具有可逆热色性的原因；设计一个简单的实验来验证这种分析。

1．计算该配合物X的相对分子质量；2．写出该配合物的组成式；

7．在光照的情况下，A能发生分解，分解成等物质的量的一种酸性气体和一种活性很高的物质C。

第六题(12分) 核磁共振成像技术是一种用精确的、非入侵的方法对人体内部器官进行成像的技术，对于医学诊断、治疗和康复非常重要。保罗 · 劳特布尔和彼得 · 曼斯菲尔德因在核磁共振成像技术领域的突破性成就而获2003年诺贝尔生理学奖与医学奖。核磁共振成像技术还可用于研究生物化学，如研究核酸与配体之间的相互作用，核酸与蛋白质分子、核酸与小分子药物的相互做作用等。

　 通常质子数和中子数之和为奇数的核，如等的核，最适合于核磁共振检测。某些过渡金属元素原子的核在低氧化态时，适合于核磁共振检测，而在较高氧化态时，无法得到可辩认的核磁图谱。

　 今有一含某过渡金属M的药物，与DNA作用后可得到较好分辨率的核磁图谱。该药物水溶液在空气中被氧化后，颜色明显加深，再与DNA作用时核磁图谱严重加宽难以辨认。已知M有两种常见氧化态和两种同位素，同位素丰度分别为69%和31%。

　 金属M的化合物A，是一种不溶于水、稀乙酸及氢氧化钠溶液的黑色固体。A易溶于热盐酸，生成B的绿色溶液，B的绿色溶液与铜丝一起煮沸，逐渐变成C的棕黑色溶液，若再用大量的水稀释，则生成白色沉淀D，D可溶于氨水，生成E的无色溶液，若暴露于空气中，则迅速变成F的蓝色溶液，遇时，F遇KCN时，蓝色消失，生成G的溶液，往该溶液中加入锌粉，则生成金属M。

　 影响含金属M的口服药物药效的因素很多，其中该药物在水中的溶解度是转运它至所作用的生物膜表面的首要条件，但药物扩散穿透脂质性生物膜而作用于病变DNA的能力，还取决于药物在脂质中的溶解度，人们在设计药物时希望药物在脂/水中分配系数适中，以提高药物的药效。请回答下列问题：

6-1 该过渡金属M可能为______元素，含M的药物可获得较好的分辨率核磁图谱的原因是：

___________________________________________________________________________。

6-2 请写出该药物水溶液在空气中被氧化的离子方程式并配平__________________________　　　 _____　

6-3 请指出字母A、B、C、D、E、F所代表的物质的化学式

A________ 　B________C_________D__________E___________F____________

6-4 若将含金属M的药物作为口服药设计，若要增加其脂溶性，可引入的基团有_____________________；若要增加其水溶性，可引入的集团有_______________________________________________________。

第[i]题(8分)皮考林酰胺及其金属配合物具有优良的配位性能和生物活性。所以，近些年来关于它们的合成及性能研究引起人们的广泛关注。同时，因配合物分子间弱的相互作用，在生物、化学、材料科学以及在分子自组装等方面扮演着重要的角色。某研究者合成了一个新超分子化合物X，步骤如下：称取0.5mmol Co(NO₃)₂·6H₂O用10mL无水乙醇溶解使呈透明溶液，然后加入含1mmol吡啶甲酰胺的乙醇溶液5mL，60℃下回流1h，过滤。室温放置，几天后析出橘红色晶体X。X属单斜晶系，晶胞参数：a＝0.695nm、b＝1.122nm、c＝1.204nm，β＝97.7°，Z＝2，ρ＝1.653g/cm³。配合物X基本单元中含有一个Co(Ⅱ)离子，为六配位的畸变的关于中心对称的八面体构型。

6．A能与联氨发生氧化还原反应。

5．A能与乙醛发生反应，产物之一为B。B既能与酸性氧化物反应，又能与碱性氧化物反应。

4．A能与NH₃反应，产物之一是酸性气体。

3．氨基丙酸能与A反应，其产物之一是碱性气体。

2．让液氨与叔丁基次氯酸盐反应也可以制备A。试写出化学反应方程式。

在A中，氮－氯键的极性非常小，这种键易被适合的反应试剂在不同的方向极化。因此一种情况是带负电端可能是氯，而在另一种情况下也可能是氮。试写出下列反应方程式：

1．试写出化学反应方程式。

例1. 2000年全国高考天津理科卷(13)

某厂生产电子元件，其产品的次品率为5%，现从一批产品中任意连续取出2件，其中次品数x 的概率分布是　　　　

解：大批产品中抽取产品，认为次品数x 服从二项分布B(2, 0.05)

空格中应填 0.9025, 0.095, 0.0025

考点：离散型随机变量的概率分布，二项分布

例2. 2001年全国高考天津理科卷(14)

一个袋子里装有大小相同的3个红球和2个黄球，从中同时取出两个，则其中含红球个数的数学期望是__________________.

解1：同时取出的两个球中含红球数 x 的概率分布为

P(x = 0) ==,　 P(x = 1) =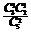=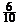,　 P(x = 2) ==

Ex ==, 空格中应填

解2：同时取出的两个球中含红球数 x 服从超几何分布，其数学期望为 n==

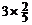例3. 2002年全国高考天津文科卷(15)

甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如下(单位：t / hm²)

其中产量比较稳定的小麦品种是　　 甲　　 。

提示：¯_甲 = 1 5( 9.8 + 9.9 + 10.1 + 10 + 10.2) = 10.0，¯_乙 = 1 5( 9.4 + 10.3 + 10.8 + 9.7 + 9.8) = 10.0;

s 2甲 = 1 5( 9.8² + … + 10.2²) – 10² = 0.02，s 2甲 = 1 5( 9.4² + … + 9.8²) – 10² = 0.244 > 0.02 。

例4. 2003年全国高考江苏卷(14)　 辽宁卷(14)　 天津文科卷(14)　 天津理科卷(14)

某公司生产三种型号的轿车，产量分别为1200辆，6000辆和2000辆。为检验该公司的产品质量，现用分层抽样的方法抽取46辆进行检验，这三种型号的轿车依次应抽取　 6　 ，z　 30　 ，　 10　 辆。　

提示：1200 + 6000 + 2000 = 9200；46 : 9200 = 1 : 20；

\ 1200 ´ 1 20 = 6，6000 ´ 1 20 = 30，2000 ´ 1 20 = 10。

例5.　 抽样本检查是产品检查的常用方法.分为返回抽样和不返回抽样两种具体操作方案.现有100只外型相同的电路板，其中有40只A类版后60只B类板.问在下列两种情况中“从100只抽出3只，3只都是B类”的概率是多少？

⑴ 每次取出一只，测试后放回，然后再随机抽取下一只(称为返回抽样)；

⑵ 每次取出一只，测试后不放回，在其余的电路板中，随意取下一只(称为不返回抽样)

解：⑴ 设“从100只中抽去3只，3只都是B类”为事件M，先求基本事件总数，由于每次抽去一只，测试后又放回，故每次都是从100只电路板中任取一只，这是重复排列，共有

个.再求M所包含的基本事件数，由于每次抽出后又放回，故是重复排列，共有 个，所以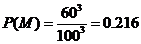

⑵ 由于取出后不放回，所以总的基本事件数为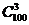个，事件M的基本事件数为，所以

例6. 　已知连续型随机变量ε的概率密度函数，且f(x) ≥0，求常数k的值，并计算概率P(1.5≤ε<2.5)。

　 分析:凡是计算连续型随机变量ε的密度函数f(x)中的参数、概率P(a≤ε≤b)都需要通过求面积来转化而求得。若f(x) ≥0且在[a，b]上为线性，那么P(a≤ε≤b)的值等于以b-a为高，f(a)与f(b)为上、下底的直角梯形的面积，即。

　解:　 ∵

　∴；

　例7. 　对划艇运动员甲、乙二人在相同的条件下进行了6次测试，测得他们最大速度的数据如下：

　甲：27，38，30，37，35，31；

　乙：33，29，38，34，28，36。

　根据以上数据，试判断他们谁更优秀。

　分析:根据统计知识可知，需要计算两组数据的与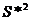，然后加以比较，最后再作出判断。

　解:　 ，

；

　，

　∴，，

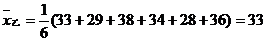　由此可以说明，甲、乙二人的最大速度的平均值相同，但乙比甲更稳定，故乙比甲更优秀。

　说明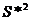：与作为总体方差的两个估计量，当样品容量不是很大时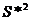，更接近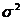，故在实际运用时，我们常用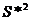去估计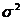，但当容量较大时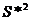，与则没有什么差别。

例8．几何分布

某射击手击中目标的概率为P。求从射击开始到击中目标所需次数的期望、方差。

解：

	1	2	3	……		……

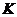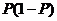令 　

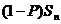
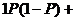
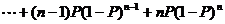
　例9．设，且总体密度曲线的函数表达式为：

　，x∈R。

　(1)求μ，σ；(2)求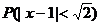及的值。

　分析：根据表示正态曲线函数的结构特征，对照已知函数求出μ和σ。利用一般正态总体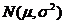与标准正态总体N(0，1)概率间的关系，将一般正态总体划归为标准正态总体来解决。

　解：　 (1)由于，根据一般正态分布的函数表达形式，可知μ=1，，故X-N(1，2)。

　(2)

　　　　　　　　　　 。

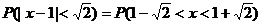
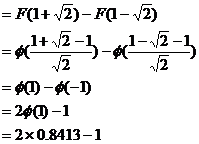
　又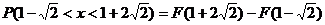

　　　　　　　　　　　　　 。

　说明：在解决数学问题的过程中，将未知的，不熟悉的问题转化为已知的、熟悉的、已解决了的问题，是我们常用的手段与思考问题的出发点。通过本例我们还可以看出一般正态分布与标准正态分布间的内在关联。

　例10．公共汽车门的高度是按照确保99%以上的成年男子头部不跟车门顶部碰撞设计的，如果某地成年男子的身高ε-N(173，7)(单位：cm)，问车门应设计多高(精确到1cm)？

　分析：由题意可知，求的是车门的最低高度，可设其为xcm，使其总体在不低于x的概率小于1%。

　解：设该地区公共汽车车门的最低高度应设为xcm，由题意，需使P(ε≥x)<1%。

　∵ε-N(173，7)，∴。查表得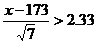，解得x>179.16，即公共汽车门的高度至少应设计为180cm，可确保99%以上的成年男子头部不跟车门顶部碰撞。

　说明：解决本题的关键是在正确理解题意的基础上，找出正确的数学表达式；而逆向思维和逆向查表，体现解决问题时思维的灵活性。

　例11．已知某地每单位面积菜地年平均使用氮肥量xkg与每单位面积蔬菜年平均产量yt之间的关系有如下数据：

　(1)求x与y之间的相关系数，并检验是否线性相关；

　(2)若线性相关，求蔬菜产量y与使用氮肥量之间的回归直线方程，并估计每单位面积施肥150kg时，每单位面积蔬菜的年平均产量。

　分析：(1)使用样本相关系数计算公式来完成；(2)查表得出显著性水平0.05与自由度15-2相应的相关系数临界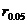比较，若则线性相关，否则不线性相关。

　解：(1)列出下表，并用科学计算器进行有关计算：]

i	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
	70	74	80	78	85	92	90	95	92	108	115	123	130	138	145
	5.1	6.0	6.8	7.8	9.0	10.2	10.0	12.0	11.5	11.0	11.8	12.2	12.5	12.8	13.0
	357	444	544	608.4	765	938.4	900	1140	1058	1188	1357	1500.6	1625	1766.4	1885

　，，

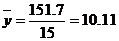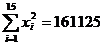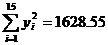　，，。故蔬菜产量与放用氮肥量的相关系数

　。

　由于n=15，故自由度15-2=13。由相关系数检验的临界值表查出与显著水平0.05及自由度13相关系数临界值，则，从而说明蔬菜产量与氮肥量之间存在着线性相关关系。

　(2)设所求的回归直线方程为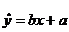，则，

　，

　∴回归直线方程为。

　说明：求解两个变量的相关系数及它们的回归直线方程的计算量较大，需要细心、谨慎地计算。如果会使用含统计的科学计算器，能简单得到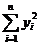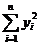，，，，这些量，也就无需有制表这一步，直接算出结果就行了。另外，利用计算机中有关应用程序也可以对这些数据进行处理。

例12.设随机变量ε服从N(0，1)，求下列各式的值：

　(1)P(ε≥2.55)；　　 (2)P(ε<-1.44)；　　 (3)P(|ε|<1.52)。

　分析:一个随机变量若服从标准正态分布，可以借助于标准正态分布表，查出其值。但在标准正态分布表中只给出了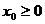，即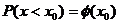的情形，对于其它情形一般用公式：φ(-x)=1-φ(x)；p(a<x<b)= φ(b)- φ(a)及等来转化。

　解:(1)

　(2)

　　　　　　　　　 ；

　(3)

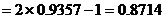
说明：从本题可知，在标准正态分布表中只要给出了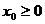的概率，就可以利用上述三个公式求出其它情形下的概率。

例13．某厂生产的圆柱形零件的外径ε-N(4，0.25)。质检人员从该厂生产的1000件零件中随机抽查一件，测得它的外径为5.7cm。试问该厂生产的这批零件是否合格？

　分析：欲判定这批零件是否合格，由假设检验基本思想可知，关键是看随机抽查的一件产品的尺寸是在(μ-3σ，μ+3σ)内，还是在(μ-3σ，μ+3σ)之外。

　解：由于圆柱形零件的外径ε-N(4，0.25)，由正态分布的特征可知，正态分布N(4，0.25)在区间(4-3×0.5，4+3×0.5)即(2.5，5.5)之外取值的概率只有0.003，而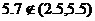，这说明在一次试验中，出现了几乎不可能发生的小概率事件，根据统计中假设检验的基本思想，认为该厂这批产品是不合格的。

说明：判断某批产品是否合格，主要运用统计中假设检验的基本思想。

例14．假设关于某设备的使用年限x和所支出的维修费用y(万元)，有如下的统计资料：

　若由资料可知y对x呈线性相关关系。试求：

　(1)线性回归方程；

　(2)估计使用年限为10年时，维修费用是多少？

　分析：本题为了降低难度，告诉了y与x间呈线性相关关系，目的是训练公式的使用。

　解：(1)列表如下：　

i	1	2	3	4	5
	2	3	4	5	6
	2.2	3.8	5.5	6.5	7.0
	4.4	11.4	22.0	32.5	42.0
	4	9	16	25	36
， ，

　于是，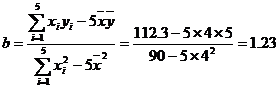

　。

　∴线性回归方程为：。

　(2)当x=10时，(万元)

　即估计使用10年时维修费用是12.38万元。

说明：本题若没有告诉我们y与x间是呈线性相关的，应首先进行相关性检验。如果本身两个变量不具备线性相关关系，或者说它们之间相关关系不显著时，即使求出回归方程也是没有意义的，而且其估计与预测也是不可信的。

例15. (2003年全国高考辽宁卷(20)　 天津理科卷(20))

A、B两个代表队进行乒乓球对抗赛，每队三名队员，A队队员是A₁、A₂、A₃，B队队员是B₁、B₂、B₃ 。按以往多次比赛的统计，对阵队员之间胜负概率如下：

现按表中对阵方式出场, 每场胜队得1分, 负队得0分。设A队、B队最后总分分别为 x、h。

(Ⅰ) 求 x、h 的概率分布；

(Ⅱ) 求Ex、Eh。

分析：本题考查离散型随机变量分布列和数学期望等概念，考查运用概率知识解决实际问题的能力。

解：(Ⅰ) x、h 的可能取值分别为3, 2, 1, 0.

　　 P(x = 3) =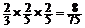　　　 　　　　　　　　　　　　　　　　　　　 (即A队连胜3场)

　　 P(x = 2) =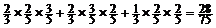　　　 　　 (即A队共胜2场)

　　 P(x = 1) =　　　 (即A队恰胜1场)

　　 P(x = 0) =　　 　　　　　　　　　 (即A队连负3场)

根据题意知 x + h = 3，所以

　 　P(h = 0) = P(x = 3) = 8 75，　　　　　 P(h = 1) = P(x = 2) = 28 75，

　 　P(h = 2) = P(x = 1) = 2 5，　　　　　 P(h = 3) = P(x = 0) = 3 25 。

(Ⅱ) Ex = ；

　　 因为x + h = 3，

　　 所以Eh = 3 – Ex =。