
用数表示形、用形表示数,用数与形的有机结合解决问题。常有:数轴划线法、数轴标根法、文氏图法、向量法、坐标法、图象法等。
㈠例题
1、已知 ,
,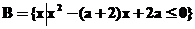 ,求满足下列条件的a的取值范围。①
,求满足下列条件的a的取值范围。① ;(答案:
;(答案: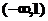 );②
);② ;(答案:[1,2]);③
;(答案:[1,2]);③ 仅有一个元素。(答案:
仅有一个元素。(答案: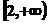 )
)
43、试确定方程 的实根所在的区间。(答案:可为(0.5,1))
的实根所在的区间。(答案:可为(0.5,1))
深夜,某市一辆出租车被牵涉进一起交通事故,该市有红色与绿色两种颜色的出租车共计2000辆,其中绿色出租车和红色出租车分别占整个城市出租车的85%和15%,据现场目击证人说,事故现场的出租车是红色的,有关部门对证人的辨别能力作了测试,测得他辩认的正确率为80%,于是警察就认定红色出租车具有较大的肇事嫌疑。①根据证人的说法,填写下列的信息表,并求红色出租车肇事的概率。(答案:P1=12/29) ②试问警察的认定对红色出租车公平吗?请说明理由。(答案:不公平;P2=17/29>P1)
|
|
证人所说的颜色(正确率80%) |
|||
|
真实颜色 |
|
绿色(辆) |
红色(辆) |
合计(辆) |
|
绿色(85%) |
|
|
|
|
|
红色(15%) |
|
240 |
|
|
|
合计(辆) |
|
|
2000 |
42、已知函数 ,
, ,求
,求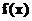 的最小值。(答案:0)
的最小值。(答案:0)
41、已知双曲线 的左,右焦点分别为
的左,右焦点分别为 、
、 ,点P在双曲线的右支上,且
,点P在双曲线的右支上,且 ,求此双曲线的离心率e的最大值。(答案:5/3)
,求此双曲线的离心率e的最大值。(答案:5/3)
40、集M={ |
| },N={
},N={
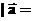
 ,求
,求 。
。
(答案:(1,1)
39、已知复数 为虚数单位),求复数点Z的轨迹方程。(答案:
为虚数单位),求复数点Z的轨迹方程。(答案: )
)
38、二次函数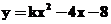 在区间[5,20]上是增加的,求实数
在区间[5,20]上是增加的,求实数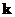 的取值范围。(答案:
的取值范围。(答案: )
)
37、若△ABC的一个顶点为椭圆 (a>b>0)短轴的一个端点,另两个顶点在椭圆上,且△ABC的重心恰好为椭圆的一个焦点,求椭圆的离心率的取值范围。(答案:
(a>b>0)短轴的一个端点,另两个顶点在椭圆上,且△ABC的重心恰好为椭圆的一个焦点,求椭圆的离心率的取值范围。(答案: )
)
36、甲、乙两位国际象棋选手在一次比赛中对局,赛前分析,甲胜的概率比乙胜的概率高6%,甲、乙和棋的概率为58%,求甲胜的概率。(答案:0.24)
35、在 的展开式中含
的展开式中含 的项的系数是首项为-2,公差为3的等差数列的第几项?(答案:20)
的项的系数是首项为-2,公差为3的等差数列的第几项?(答案:20)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com