4．某瓜农采用大棚栽培技术种植了一亩地的良种西瓜，这亩地西瓜约600个，在西瓜上市时随机摘了10个成熟的西瓜，称得如下：

则这10个西瓜的平均质量是　　　　　　　　　　 千克，这亩地西瓜产量约是　　　　　　　 千克。

3．一组数据中的每一个数据都减去80，得一组新数据，若求得新数据的平均数是1.2，方差是4.4，则原来数据的平均数是　　　　　　　　　　 ，方差是　　　　　　　　　　 ．

2．某班有50名学生，某次数学考试的成绩经计算得到的平均分数是70分，标准差是S，后来发现记录有误，某甲得70分误记为40分，某乙50分误记为80分，更正后重新计算得标准差为S₁，则S与S₁之间的关系是　　　　　　　　　　　　　　

作业

1．如果两组数和的样本平均数分别是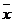和，那么一组数的平均数是　　　　　　　　　　　　　　　　

6．某人5次上班途中所花的时间(单位：分钟)分别为x,y,10,11,9，已知这组数据的平均数为10，方差为2，则的值为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

例题讲解

例1．某赛季甲、乙两名篮球运动员每场比赛得分情况如下：　　

甲的得分：12，15，24，25，3l，31，36，36，37，39，44，49，50；

乙的得分：8，13，14，16，23，26，28，33，38，39，59．

(1)制作茎叶图，并对两名运动员的成绩进行比较；

(2)计算上述两组数据的平均数和方差，并比较两名运动员的成绩和稳定性；

(3)能否说明甲的成绩一定比乙好，为什么?

例2．为了解某校初中毕业男生的体能状况，从该校初中毕业班学生中抽取若干名男生进行铅球测试，把所得数据(精确到0．1米)进行整理后，分成6组画出频率分布直方图的一部分(如下图)已知从左到右前5个小组的频率分别为0.04，0.10，0.14，0.28，0.30．第6小组的频数是7．

(1)请将频率分布直方图补充完整；

(2)该校参加这次铅球测试的男生有多少人?

(3)若成绩在8．0米以上(含8．0米)的为合格，试求这次铅球测试的成绩的合格率；

(4)在这次测试中，你能确定该校参加测试的男生铅球成绩的众数和中位数各落在哪个小组内吗?

5．期中考试以后，班长算出了全班40个人数学成绩的平均分为M，如果把M当成一个同学的分数，与原来的40个分数一起，算出这41个分数的平均值为N那么为　　　　　　　　　　　　　

4．某商贩有600千克苹果出售，有以下两个出售方案：

①分成甲级200千克，每千克售价2.40元，乙级400千克，每千克售价1.20元；

②分成甲级400千克，每千克售价2.00元，乙级200千克，每千克售价1.00元。

两种出售方案的平均价格分别为和，则与的关系为　　　　　　　　　　　　　　　

3．如果数据的平均数为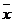，方差为S²，则的平均数和方差分别为　　　　　　 　　　　　　　　　　

2．已知5个数据3，5，7，4，6，则该样本标准差为　　　　　　　　　　　　　　　

1．已知一组数据为20、30、40、50、50、60、70、80，其平均数、中位数和众数分别为