4．设e₁，e₂是两个单位向量，它们的夹角为60°，则(2e₁－e₂)(3e₁+2e₂)＝　　　 .

3．已知|a|²＝1，|b|²＝2，(a－b)⊥a，则a与b的夹角为　　　　　　　　　　　　 (　　 )

A.60°　　　　　　　　　　　 　　 B.90°　　　　　　　 C.45°　　　　　　　　　　　 D.30°　

2．已知等边△ABC的边长为1，且＝a，＝b，＝c，则a·b+b·c+c·a等于　 (　　 )

A.－　　　　　　　　　　　　　　 　　B. 　　　　　　　　　C.0　　　　　　　　　　　　　　　　　 D. 　　

1．△ABC中，＝a，＝b，且a·b＞0，则△ABC为　　　　　　　　　　　　 (　　 )

A.锐角三角形　　　　　 B.直角三角形　　　 C.钝角三角形　　　　 　 D.等腰直角三角形　

5．已知|a|＝3，|b|＝4，(a+b)·(a+3b)＝33，则a与b的夹角为　　　　　　　 (　　 )

A.30°　　　　　　　　　　　　　　　 B.60°　　　　　　　 C.120°　　　　　　　　　　　　　 　 D.150°　

[典型例题讲练]

例1、　　　 已知：｜a｜＝3，｜b｜＝6，当①a∥b，②a⊥b，③a与b的夹角是60°时，分别求a·b.

变式：设e₁，e₂是两个单位向量，它们的夹角为60°，则(2e₁－e₂)(3e₁+2e₂)＝　　　 .

例2已知a、b都是非零向量，且a+3b与7a－5b垂直，a－4b与7a－2b垂直，求a与b的夹角.

变式: 已知｜a｜＝2，｜b｜＝5，a·b＝－3，求｜a+b｜，｜a－b｜.

[课堂小结]

掌握平面向量数量积运算规律，能利用数量积的5个重要性质及数量积运算规律解决有关问题，掌握两个向量共线、垂直的几何判断，会证明两向量垂直，以及能解决一些简单问题.

[课堂检测]

4．设a，b，c为任意非0向量，且相互不共线，则真命题为　　　　　　　　　　 (　　 )

(1)(a·b)·c－(c·a)·b＝0　　　　　　　 (2)|a|－|b|＜|a－b|

(3)(b·c)·a－(c·a)·b不与c垂直　　　　 (4)(3a+2b)(3a－2b)=9|a|²－4|b|²

A.(2)(4)　　　　　　 B.(2)(3)　　　　 C.(1)(2)　　　　　　　 D.(3)(4)　　

3．已知｜a｜＝2，｜b｜＝3，a与b的夹角为90°，则a·b=_________

2. 已知△ABC中，a＝5，b＝8，C＝60°，则·=__________

1. 判断正误，并简要说明理由.

①a·0＝0；②0·a＝0；③0－＝；④｜a·b｜＝｜a｜｜b｜；⑤若a≠0，则对任一非零b有a·b≠0；⑥a·b＝0，则a与b中至少有一个为0；⑦对任意向量a，b，c都有(a·b)c＝a(b·c)；⑧a与b是两个单位向量，则a²＝b².⑨a·b>0，则它们的夹角为锐角。

4.两向量垂直的坐标表示：设a＝(x₁，y₁)，b＝(x₂，y₂)，则a⊥b___________.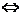

[基本训练]