
4.已知函数 (
(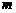 为常数)图象上
为常数)图象上 处的切线与
处的切线与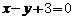 的夹角为
的夹角为 ,则
,则 点的横坐标为
.
点的横坐标为
.
3.曲线 与
与 在交点处切线的夹角是____ __.
在交点处切线的夹角是____ __.
2.若曲线 的一条切线
的一条切线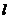 与直线
与直线 垂直,则
垂直,则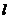 的方程为 .
的方程为 .
2.试比较正弦函数y=sinx在区间 和
和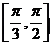 上的平均变化率,并比较大小。
上的平均变化率,并比较大小。
§62 导数的概念及导数的几何意义⑵
[典型例题讲练]
例2.自由落体运动的物体的位移s(单位:s)与时间t(单位:s)之间的关系是:s(t)= gt2(g是重力加速度),求该物体在时间段[t1,t2]内的平均速度;
gt2(g是重力加速度),求该物体在时间段[t1,t2]内的平均速度;
练习:自由落体运动的位移s(m)与时间t(s)的关系为s=
(1)求t=t0s时的瞬时速度;(2)求t=3s时的瞬时速度;
(3)求t=3s时的瞬时加速度;
例3.已知f(x)=x2,求曲线在x=2处的切线的斜率。
练习:1. 曲线y=x3在点P处切线斜率为k,当k=3时,P点的坐标为_________.
1.求函数 在区间[1,1+△x]内的平均变化率
在区间[1,1+△x]内的平均变化率
3.在高台跳水运动中,运动员相对于水面高度与起跳的时间t的函数关系为 ,则 ( )
,则 ( )
A.  B.
B. 
C. 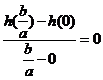 D.运动员在
D.运动员在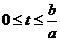 这段时间内处于静止状态
这段时间内处于静止状态
[典型例题讲练]
例1.已知函数f(x)=2x+1,
⑴分别计算在区间[-3,-1],[0,5]上函数f(x)的平均变化率;
⑵.探求一次函数y=kx+b在区间[m,n]上的平均变化率的特点;
练习:已知函数f(x)=x2+2x,分别计算f(x)在下列区间上的平均变化率;
⑴[1,2]; ⑵[3,4]; ⑶[-1,1]; ⑷[2,3]
[课堂检测]
2.A、B两船从同一码头同时出发,A船向北,B船向东,若A船的速度为30km/h,B船的速度为40km/h,设时间为t,则在区间[t1,t2]上,A,B两船间距离变化的平均速度为____ __ _
1.已知函数 在区间[1,2]上的平均变化率为
在区间[1,2]上的平均变化率为 ,则
,则 在区间[-2,-1]上的平均变化率为 .
在区间[-2,-1]上的平均变化率为 .
4.瞬时速度与瞬时加速度:位移的平均变化率: ,称为
;当
,称为
;当 无限趋近于0 时,
无限趋近于0 时, 无限趋近于一个常数,这个常数称为t=t0时的
;速度的平均变化率:
无限趋近于一个常数,这个常数称为t=t0时的
;速度的平均变化率: ,当
,当 无限趋近于0 时,
无限趋近于0 时, 无限趋近于一个常数,这个常数称为t=t0时的
.
无限趋近于一个常数,这个常数称为t=t0时的
.
[基础练习]
3.曲线上任一点(x0,f(x0))切线斜率的求法: ,当
,当
△x无限趋近于0时,k值即为(x0,f(x0))处切线的 ,记为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com