
1.若函数 在区间
在区间 内是一个可导函数,则
内是一个可导函数,则 >0是
>0是 在区间
在区间 内递增的
条件.
内递增的
条件.
4.求可导函数 在
在 上的最大或最小值的一般步骤和方法:
上的最大或最小值的一般步骤和方法:
①求函数 在
在 上的值;②将极值与区间端点的函数值
上的值;②将极值与区间端点的函数值 比较,确定最值。
比较,确定最值。
[基础练习]
3.函数极值的定义:设函数 在点
在点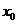 附近有定义,如果对
附近有定义,如果对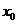 附近的所有点,都有
附近的所有点,都有 (或
(或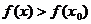 ),就说
),就说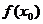 是函数
是函数 的一个极
值;
和
统称为极值;
的一个极
值;
和
统称为极值;
2.求可导函数单调区间的一般步骤和方法:
⑴确定函数 的 ;⑵求
的 ;⑵求 ,令
,令 ,解此方程,求出它在定义域外区间内的一切
;
,解此方程,求出它在定义域外区间内的一切
;
⑶把上面的各实根按由
的顺序排列起来,然后用这些点把函数 的定义区间分成若干个小区间;
的定义区间分成若干个小区间;
⑷确定 在各个小区间内的符号,根据
在各个小区间内的符号,根据 的 判断函数
的 判断函数 在每个相应小区间内的增减性;
在每个相应小区间内的增减性;
1.用导数的符号判别函数增减性的方法:若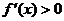 ,则函数
,则函数 为
,若
为
,若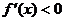 ,则函数
,则函数 为
;
为
;
4.已知抛物线y=ax2+bx+c通过点(1,1),且在点(2,-1)处与直线y=x-3相切,求a、b、c的值.
3.设函数f(x)=ax3+3x2+2,若f′(-1)=4,试求a的值.
2.求下列函数的导数:(1) y=lg(1+cos2x) (2) y=exlnx
1.若曲线y=x2-1与y=1-x3在x=x0处的切线互相垂直,则x0等于 .
5.已知曲线y= 和这条曲线上的一点P(2,
和这条曲线上的一点P(2, ),求曲线y=
),求曲线y= 在点P处的切线方程.
在点P处的切线方程.
[课堂作业]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com