1．若函数f(x)=x³+x²+mx+1是R上的单调函数，则实数m的取值范围是______________．

3．与实际生活有关的最值问题：

例3．在经济学中，生产x单位产品的成本称为成本函数同，记为C(x)，出售x单位产品的收益称为收益函数，记为R(x)，R(x)－C(x)称为利润函数，记为P(x)。

(1)．如果C(x)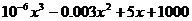＝，那么生产多少单位产品时，边际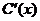最低？(边际成本：生产规模增加一个单位时成本的增加量)

(2)．如果C(x)=50x+10000，产品的单价P＝100－0.01x，那么怎样定价，可使利润最大？

变式：已知某商品生产成本C与产量q的函数关系是：C＝100+4q，价格P与产量q的函数关系为P＝25－，求产量q为何值时，利润L最大？

[课堂检测]：

3．请您设计一个帐篷。它下部的形状是高为1m的正六棱柱，上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心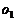的距离为多少时，帐篷的体积最大？

§68导数在实际生活中的应用⑵

[典型例题讲练]

2．如图，把边长为a的正六边形纸板剪去相同的六个角，做成一个底面为正六边形的无盖六棱柱盒子，设高为h所做成的盒子体积V(不计接缝).

(1)写出体积V与高h的函数关系式；

(2)当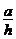为多少时，体积V最大，最大值是多少？

1．用边长为48厘米的正方形铁皮做一个无盖的铁盒时，在缺皮的四角各截去一个面积相等的小正方形后把四边折起焊成铁盒，所做铁盒容积最大时，截去的正方形的边长为_____________。

2．与物理学有关的最值问题；

例2．统计表明，某种型号的汽车在匀速行驶中每小时的耗油量(升)关于行驶速度(千米/小时)的函数解析式可以表示为：已知甲乙两地相距100千米。

(Ⅰ)当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？

(Ⅱ)当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？

[课堂检测]：

1．与几何有关的最值问题：

例1．在边长为60cm的正方形铁皮的四角切去边长相等的正方形，再把它的边沿虚线折起，做成一个无盖的方底的铁皮箱，箱底边长为多少时，箱子容积最大？最大容积是多少？

练习：某种圆柱形饮料罐的容积为V，如何确定它的高与底半径，才能使它的用料最省？

变式1：表面积为定值S，如何制造，才能使其容积最大？

变式2：例中若罐底单位造价为周围单位造价为侧壁部分单位造价的2倍，如何设计尺寸，使总造价最低？

变式3：有一底半径为r(cm)，高为h(cm)的倒立的圆锥容器，若以n(cm³)/s的速度向容器里注水，求注水t(s)的水面上长的速度。

6. 已知是函数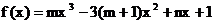的一个极值点, 其中

(1) 求m与n的关系式;　　 (2) 求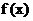的单调区间;

(3) 当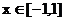时, 函数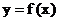的图象上任意一点的切线斜率恒大于3m, 求m的取值范围.

5．已知函数y=3x³+2x²－1在区间(m，0)上是减函数，则m的取值范围是_____________

4．设函数y=f(x)是一次函数，已知f(0)=1，f(1)=－3，则该函数的导数

f′(x)=　　　　 ．