
3.形如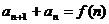 型
型
(1)若 (d为常数),则数列{
(d为常数),则数列{ }为“等和数列”,它是一个周期数列,周期为2,其通项分奇数项和偶数项来讨论;
}为“等和数列”,它是一个周期数列,周期为2,其通项分奇数项和偶数项来讨论;
(2)若f(n)为n的函数(非常数)时,可通过构造转化为 型,通过累加来求出通项;或用逐差法(两式相减)得
型,通过累加来求出通项;或用逐差法(两式相减)得 ,,分奇偶项来分求通项.
,,分奇偶项来分求通项.
例1. 数列{ }满足
}满足 ,
, ,求数列{an}的通项公式.
,求数列{an}的通项公式.
分析 1:构造 转化为 型
型
解法1:令
则 .
.
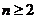 时,
时,
各式相加:
当n为偶数时, .
.
此时
当n为奇数时,
此时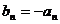 ,所以
,所以 .
.
故 

解法2:



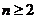 时,
时,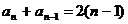 ,
,
两式相减得: .
.

 构成以
构成以 ,为首项,以2为公差的等差数列;
,为首项,以2为公差的等差数列;
 构成以
构成以 ,为首项,以2为公差的等差数列
,为首项,以2为公差的等差数列


 .
.


评注:结果要还原成n的表达式.
例2.(2005江西卷)已知数列{an}的前n项和Sn满足
Sn-Sn-2=3 求数列{an}的通项公式.
求数列{an}的通项公式.
解:方法一:因为
以下同例1,略
答案 
2.形如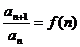 型
型
(1)当f(n)为常数,即: (其中q是不为0的常数),此时数列为等比数列,
(其中q是不为0的常数),此时数列为等比数列, =
=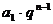 .
.
(2)当f(n)为n的函数时,用累乘法.
由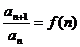 得
得 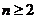 时,
时, ,
,

 =f(n)f(n-1)
=f(n)f(n-1) .
.
例1.设 是首项为1的正项数列,且
是首项为1的正项数列,且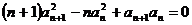 (
(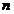 =1,2, 3,…),则它的通项公式是
=1,2, 3,…),则它的通项公式是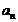 =________.
=________.
解:已知等式可化为:

 (
(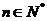 )
) (n+1)
(n+1) , 即
, 即

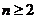 时,
时,

 =
= =
= .
.
评注:本题是关于 和
和 的二次齐次式,可以通过因式分解(一般情况时用求根公式)得到
的二次齐次式,可以通过因式分解(一般情况时用求根公式)得到 与
与 的更为明显的关系式,从而求出
的更为明显的关系式,从而求出 .
.
例2.已知 ,求数列{an}的通项公式.
,求数列{an}的通项公式.
解:因为 所以
所以
故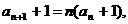 又因为
又因为 ,即
,即 ,
,
所以由上式可知 ,所以
,所以 ,故由累乘法得
,故由累乘法得
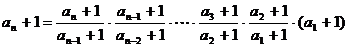
=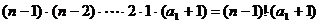
所以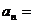
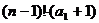 -1.
-1.
评注:本题解题的关键是把原来的递推关系式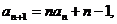 转化为
转化为
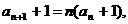 若令
若令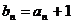 ,则问题进一步转化为
,则问题进一步转化为 形式,进而应用累乘法求出数列的通项公式.
形式,进而应用累乘法求出数列的通项公式.
除以上的转化方式外,还会出现多栋楼之间的联系,即不同数列之间的递推关系,对于该类问题,要整体考虑,根据所给数列递推公式的关系,灵活采用累加、累乘、化归等方法求解。
例题9:甲、乙两容器中分别盛有浓度为10%、20%的某种溶液500ml,同时从甲乙两个容器中取出100ml溶液,将近倒入对方的容器搅匀,这称为是一次调和,记a1=10%,b1=20%,经(n-1)次调和后甲、乙两个容器的溶液浓度为an、bn,
(1)试用an-1、bn-1表示an、bn;
(2)求证数列 {an-bn}是等比数列,并求出an、bn的通项。
分析:该问题属于数列应用题,涉及到两个不同的数列an和bn,且这两者相互之间又有制约关系,所以不能单独地考虑某一个数列,而应该把两个数列相互联系起来。
解析:(1)由题意
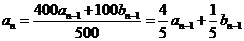 ;
; 
(2)an-bn= =
=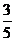 (
(
 )(n≥2), ∴{an-bn}是等比数列。
)(n≥2), ∴{an-bn}是等比数列。
又a1-b1=-10% ∴an-bn=-10%( n-1
………(1)
n-1
………(1)
又∵
 =
=
 =…= a1+b1=30% ………(2)
=…= a1+b1=30% ………(2)
联立(1)、(2)得 =-(
=-( n-1·5%+15%;
n-1·5%+15%;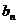 =(
=( n-1·5%+15%。
n-1·5%+15%。
综而言之,等差、等比数列是两类最基本的数列,是数列部分的重点,自然也是高考考查的热点,而考查的目的在于测试灵活运用知识的能力,这个“灵活”往往集中在“转化”的水平上;以上介绍的仅是常见可求通项的递推数列的五种转化思路----“楼层式”的转化方式,同样采用相应的、风趣的教学形式,更易于学生接收新知识,从而激发学生的学习兴趣,让数学课堂生动活泼风趣起来。这正顺应了当前“新课程理念”的大趋势。
利用递推关系求数列通项的九种类型及解法
1.形如 型
型
(1)若f(n)为常数,即: ,此时数列为等差数列,则
,此时数列为等差数列,则 =
= .
.
(2)若f(n)为n的函数时,用累加法.
方法如下: 由  得:
得:
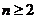 时,
时, ,
,
 ,
,



所以各式相加得 
即: .
.
为了书写方便,也可用横式来写:

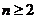 时,
时, ,
,

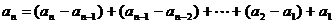
= .
.
例 1. (2003天津文) 已知数列{an}满足 ,
,
证明
证明:由已知得:

=

 .
.
例2.已知数列 的首项为1,且
的首项为1,且 写出数列
写出数列 的通项公式.
答案:
的通项公式.
答案:
例3.已知数列 满足
满足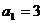 ,
, ,求此数列的通项公式.
答案:
,求此数列的通项公式.
答案:
评注:已知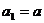 ,
, ,其中f(n)可以是关于n的一次函数、二次函数、指数函数、分式函数,求通项
,其中f(n)可以是关于n的一次函数、二次函数、指数函数、分式函数,求通项 .
.
①若f(n)是关于n的一次函数,累加后可转化为等差数列求和;
②若f(n)是关于n的二次函数,累加后可分组求和;
③若f(n)是关于n的指数函数,累加后可转化为等比数列求和;
④若f(n)是关于n的分式函数,累加后可裂项求和。
例4.已知数列 中,
中,  且
且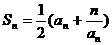 ,求数列
,求数列 的通项公式.
的通项公式.
解:由已知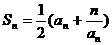 得
得 ,
,
化简有 ,由类型(1)有
,由类型(1)有 ,
,
又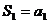 得
得 ,所以
,所以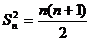 ,又
,又 ,
,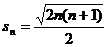 ,
,
则
此题也可以用数学归纳法来求解.
若数列 满足关系
满足关系 ,由这个递推关系及初始值确定的数列,也是递推数列。它主要给出的是“二层”与“三层”之间的递推关系式,解决途径是利用
,由这个递推关系及初始值确定的数列,也是递推数列。它主要给出的是“二层”与“三层”之间的递推关系式,解决途径是利用 转化为纯粹的“二层”或“三层”问题,即
转化为纯粹的“二层”或“三层”问题,即 型或
型或 型(也就是将混合型的转化为纯粹型的)
型(也就是将混合型的转化为纯粹型的)
例题7:已知数列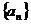 的前n项和Sn满足
的前n项和Sn满足
(Ⅰ)写出数列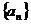 的前3项;
(Ⅱ)求数列
的前3项;
(Ⅱ)求数列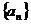 的通项公式。
的通项公式。
解析:(Ⅰ)  ---------------①
---------------①
由 得
得 ----------------②
----------------②
由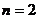 得
得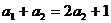 ,得
,得 --------------③
--------------③
由 得
得 ,得
,得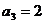 ---------④
---------④
(Ⅱ)∵ ---------------①
---------------①
∴用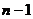 代
代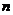 得
得
 -----------⑤
-----------⑤
由①-⑤得: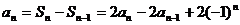
即 ----------------------------⑥
----------------------------⑥
由叠代法得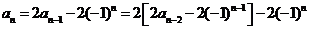

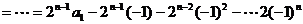
 ---------------------------⑦
---------------------------⑦
例题8:数列 的前n项和记为Sn,已知
的前n项和记为Sn,已知
证明:数列 是等比数列;(2004全国卷(二)理科19题)
是等比数列;(2004全国卷(二)理科19题)
方法(1)∵
∴  整理得
整理得 
所以  , 故
, 故 是以2为公比的等比数列.
是以2为公比的等比数列.
方法(2):事实上,我们也可以转化为 ,为一个商型的递推关系,
,为一个商型的递推关系,
由 =
=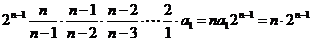
得 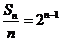 ,
下面易求证。
,
下面易求证。
当然,还有一些转化的方法和技巧,如基本式的变换,象因式分解,取倒数等还是要求掌握的。
可利用公式:
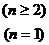 直接求出通项
直接求出通项 。
。
例题6:已知数列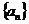 的前n项和为①
的前n项和为① ②
② ,
分别求数列
,
分别求数列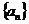 的通项公式。
的通项公式。
解析:①当 时,
时,
当 时,
时,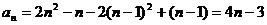
经检验  时
时
 也适合 ∴
也适合 ∴
②当 时,
时,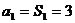
当 时,
时,
经检验  时
时
 不适合 ∴
不适合 ∴ 

若数列 满足关系
满足关系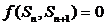 ,由这个关系式及初始值确定的数列,也可理解为递推数列。它主要给出的是“三层”中连续几项之间的递推关系式,解决途径是利用
,由这个关系式及初始值确定的数列,也可理解为递推数列。它主要给出的是“三层”中连续几项之间的递推关系式,解决途径是利用 将“三层”问题全部走下“二层”,回到
将“三层”问题全部走下“二层”,回到 型或直接能求出
型或直接能求出 ,以下过程依同上述。
,以下过程依同上述。
例题5:已知数列 的首项
的首项 ,前n项和
,前n项和 满足关系式
满足关系式 (t为常数且
(t为常数且 )
)
(1)求证:数列 是等比数列;
(2)设数列
是等比数列;
(2)设数列 的公比为
的公比为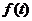 ,作数列
,作数列 ,使
,使 ,
,
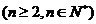 ,求
,求
解析:(1)由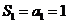 ,
, ,得
,得 ,
,
∴ ,又
,又 ,
,
得 ,得
,得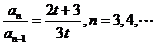
∴ 是一个首项为1,公比为
是一个首项为1,公比为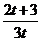 的等比数列。
的等比数列。
(2)由 ,有
,有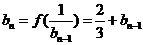
∴ 是一个首项为1,公差为
是一个首项为1,公差为 的等差数列,∴
的等差数列,∴ 。
。
类比例题:已知数列 满足
满足 ,求
,求 的通项公式。
的通项公式。
解析:记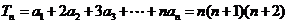
∴
∴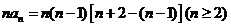 ∴
∴ 。
。
(四)数学归纳法:
例题4:已知数列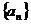 中,
中,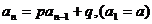 ,求通项公式
,求通项公式
解析:利用归纳、猜想、数学归纳法证明方法也可求得通项公式 。
。
即 


…

再利用数学归纳方法证明最后的结论:
①当 时,
时, 显然成立;
显然成立;
②假设当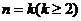 时,
时, 成立,
成立,
由题设知

即当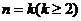 时,
时,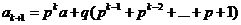 成立
成立
根据①②,当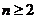 时
时 ,然后利用等比数列求和公式来化简这个通项
,然后利用等比数列求和公式来化简这个通项 。
。
(三)可以一次变形后转化为“差型”、“商型”。如: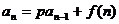 、
、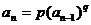 、
、 等类型。
等类型。
例题3:设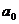 是常数,且
是常数,且 ,
,
证明: (2003年新课程理科,22题)
(2003年新课程理科,22题)
分析:这道题目是证明型的,最简单的方法当然要数数学归纳法,现在我们考虑用推导的方法来处理 的三种方法:
的三种方法:
方法(1):构造公比为-2的等比数列 ,用待定系数法可知
,用待定系数法可知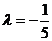
方法(2):构造差型数列 ,即两边同时除以
,即两边同时除以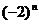 得:
得: ,从而可以用累加的方法处理。
,从而可以用累加的方法处理。
方法(3):直接用叠代的方法处理:





说明:①当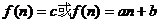 时,上述三种方法都可以用;②当
时,上述三种方法都可以用;②当 时,若用方法1,构造的等比数列应该是
时,若用方法1,构造的等比数列应该是 而用其它两种方法做则都比较难;③用叠代法关键是找出规律,除含
而用其它两种方法做则都比较难;③用叠代法关键是找出规律,除含 外的其它式子,常常是一个等比数列的求和问题。
外的其它式子,常常是一个等比数列的求和问题。
(二)由“差型”、“商型”类比出“和型”、“积型”:即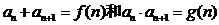
例题2:数列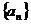 中相邻两项
中相邻两项 、
、 是方程
是方程 的两根,已知
的两根,已知
求 的值。
的值。
分析:由题意: +
+ -----①
, 生成:
-----①
, 生成:
 +
+ -----②
-----②
由②-①得:
所以该数列的所有的奇数项成等差,所有的偶数项也成等差。其基本思路是:生成、相减;与“差型”的生成、相加的思路刚好相呼应。到这里本题的解决就不在话下了。
特例:若 +
+ ,则
,则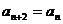 ,即该数列的所有的奇数项均相等,所有的偶数项也相等。
,即该数列的所有的奇数项均相等,所有的偶数项也相等。
若 ------① , 则
------① , 则  -------②
-------②
由②÷①得: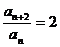
所以该数列的所有的奇数项成等比,所有的偶数项也成等比。其基本思路是:生成、相除;与“商型”的生成、相乘的思路刚好相呼应。
特例:若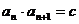 ,则
,则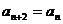 ,即该数列的所有的奇数项均相等,所有的偶数项也相等。
,即该数列的所有的奇数项均相等,所有的偶数项也相等。
(一)由等差、等比演化而来的“差型”、“商型”递推关系
(1)由等差数列演化为“差型”,如:
生成: ,
,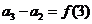 ,…,
,…, ,
,
累加: =
= ,于是只要
,于是只要 可以求和就行。
可以求和就行。
(2)由等比数列演化为“商型”,如: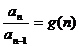
生成: ,
, ,…,
,…, ,
,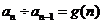
累乘:
 ,于是只要
,于是只要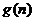 可以求积就行。
可以求积就行。
例题1:已知数列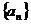 满足:
满足:
求证:① ②
② 是偶数 (《数学通讯》2004年17期P44)
是偶数 (《数学通讯》2004年17期P44)
证明:由已知可得:
又 =
=
而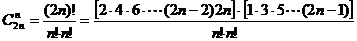 =
=
所以 ,而
,而 为偶数
为偶数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com