
3.学完“百家争鸣”有关历史后,几个同学在一起讨论本班科任老师的教学管理风格,其中借用史实评论不太恰当的是
A.小刘:数学老师是法家的弟子,学期初他就制定班规,并严格执行
B.小张:历史老师关爱学生,教育我们要和谐相处,有儒家风范
C.小汪:语文老师给我们充分的主动权,极少干预,深得老子的真传
D.小徐:政治老师很会摆架子,特别注意师道尊严,这是墨子的做法
2. 古书说:“国之大事,在祀在戎”。从下面的几幅青铜器皿图片可以看出,当时我国的青铜器主要属于:
古书说:“国之大事,在祀在戎”。从下面的几幅青铜器皿图片可以看出,当时我国的青铜器主要属于:
A.农具和酒器 B.礼器和兵器 C.礼器和用具 D.兵器和农具
1.《史记•秦始皇本纪》载:秦始皇二十六年(前 221)下令“更名民曰黔首”。秦始皇三十一年(前227)下令“使黔首自实田”。黔首之称,在战国时已经广泛使用,含义与当时常见的“民”、“庶民”相同。下列选项中同属于对百姓称呼的是①黎庶 ②苍生 ③优伶 ④氓 A.①②④ B.②③④ C.①③④ D.①②③④
9. 形如 (其中p,r为常数)型
(其中p,r为常数)型
(1)p>0, 用对数法.
用对数法.
例1. 设正项数列 满足
满足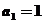 ,
, (n≥2).求数列
(n≥2).求数列 的通项公式.
的通项公式.
解:两边取对数得: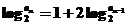 ,
, ,设
,设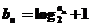 ,则
,则
 是以2为公比的等比数列,
是以2为公比的等比数列,
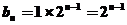 ,
, ,
, ,∴
,∴
练习 数列 中,
中,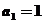 ,
,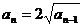 (n≥2),求数列
(n≥2),求数列 的通项公式.
答案:
的通项公式.
答案: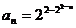
(2)p<0时 用迭代法.
例1.(2005江西卷)
已知数列
 ,
,
(1)证明 (2)求数列
(2)求数列 的通项公式an.
的通项公式an.
解:(1)略
(2)
所以 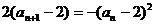
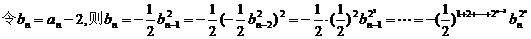 又bn=-1,所以
又bn=-1,所以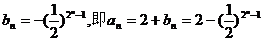 .
.
方法2:本题用归纳-猜想-证明,也很简捷,请试一试.
解法3:设c ,则c
,则c ,转化为上面类型(1)来解.
,转化为上面类型(1)来解.
8.形如 (其中p,q为常数)型
(其中p,q为常数)型
(1)当p+q=1时 用转化法
例1.数列 中,若
中,若 ,且满足
,且满足 ,求
,求 .
.
解:把 变形为
变形为 .
.
则数列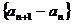 是以
是以 为首项,3为公比的等比数列,则
为首项,3为公比的等比数列,则
 利用类型6的方法可得
利用类型6的方法可得  .
.
(2)当 时 用待定系数法.
时 用待定系数法.
例2. 已知数列 满足
满足 ,且
,且 ,且满足,求
,且满足,求 .
.
解:令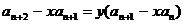 ,即
,即 ,与已知
,与已知
 比较,则有
比较,则有 ,故
,故 或
或
下面我们取其中一组 来运算,即有
来运算,即有 ,
,
则数列 是以
是以 为首项,3为公比的等比数列,故
为首项,3为公比的等比数列,故
 ,即
,即 ,利用类型 的方法,可得
,利用类型 的方法,可得
 .
.
评注:形如 的递推数列,我们通常采用两次类型(5)的方法来求解,但这种方法比较复杂,我们采用特征根的方法:设方程
的递推数列,我们通常采用两次类型(5)的方法来求解,但这种方法比较复杂,我们采用特征根的方法:设方程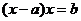 的二根为
的二根为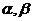 ,设
,设 ,再利用
,再利用 的值求得p,q的值即可.
的值求得p,q的值即可.
2.形如 型
型
方法:不动点法:
我们设 ,由方程
,由方程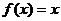 求得二根x,y,由
求得二根x,y,由 有
有
同理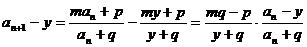 ,两式相除有
,两式相除有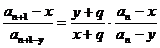 ,从而得
,从而得 ,再解出
,再解出 即可.
即可.
例1. 设数列{an}满足 ,求{an}的通项公式.
,求{an}的通项公式.
分析:此类问题常用参数法化等比数列求解.
解:对等式两端同时加参数t,得:
 ,
,
令 , 解之得t=1,-2 代入
, 解之得t=1,-2 代入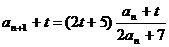 得
得
 ,
, ,
,
相除得 ,即{
,即{ }是首项为
}是首项为 ,
,
公比为 的等比数列,
的等比数列,  =
= , 解得
, 解得 .
.
方法2: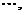
 ,
,
两边取倒数得 ,
,
令b ,则b
,则b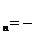
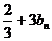 ,
,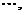 转化为类型5来求.
转化为类型5来求.
7.形如 型
型
(1)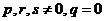 即
即 取倒数法.
取倒数法.
例1. 已知数列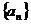 中,
中,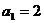 ,
, ,求通项公式
,求通项公式 。
。
解:取倒数:


例2.(湖北卷)已知不等式 为大于2的整数,
为大于2的整数, 表示不超过
表示不超过 的最大整数. 设数列
的最大整数. 设数列 的各项为正,且满足
的各项为正,且满足
(Ⅰ)证明
分析:本题看似是不等式问题,实质就是求通项问题.
证:∵当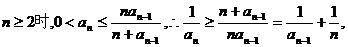
即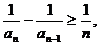 于是有
于是有 
所有不等式两边相加可得 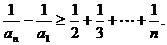
由已知不等式知,当n≥3时有,
∵
评注:本题结合不等式的性质,从两边取倒数入手,再通过裂项求和即可证得.
6.形如 型
型
.(1)若 (其中k,b是常数,且
(其中k,b是常数,且 )
)
方法:相减法
例1.
在数列 中,
中, 求通项
求通项 .
.
解: ,
, ①
①

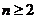 时,
时,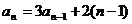 ,
,
两式相减得
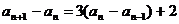 .令
.令 ,则
,则
利用类型5的方法知
即  ②
②
再由累加法可得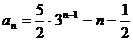 .
.
亦可联立 ① ②解出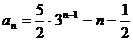 .
.
例2. 在数列 中,
中, ,求通项
,求通项 .
.
解:原递推式可化为
比较系数可得:x=-6,y=9,上式即为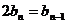
所以 是一个等比数列,首项
是一个等比数列,首项 ,公比为
,公比为 .
.
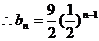 即:
即:
故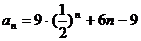 .
.
(2)若 (其中q是常数,且n
(其中q是常数,且n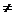 0,1)
0,1)
①若p=1时,即: ,累加即可.
,累加即可.
②若 时,即:
时,即: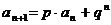 ,
,
求通项方法有以下三种方向:i. 两边同除以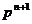 .
.
即:  ,令
,令 ,则
,则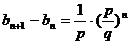 ,
,
然后类型1,累加求通项.
ii.两边同除以 . 即:
. 即: 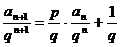 ,
,
令 ,则可化为
,则可化为 .然后转化为类型5来解,
.然后转化为类型5来解,
iii.待定系数法:
设 .通过比较系数,求出
.通过比较系数,求出 ,转化为等比数列求通项.
,转化为等比数列求通项.
例1.(2003天津理)
设 为常数,且
为常数,且 .
.
证明对任意 ≥1,
≥1, ;
;
证法1:两边同除以(-2) ,得
,得
令 ,则
,则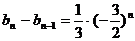

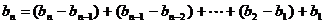
=
=
=


 .
.
证法2:由 得
得  .
.
设 ,则b
,则b . 即:
. 即: ,
,
所以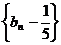 是以
是以 为首项,
为首项, 为公比的等比数列.
为公比的等比数列.
则 =
=
 ,
,
即: ,
,
故  .
.
评注:本题的关键是两边同除以3 ,进而转化为类型5,构造出新的等比数列,从而将求一般数列的通项问题转化为求等比数列的通项问题.
,进而转化为类型5,构造出新的等比数列,从而将求一般数列的通项问题转化为求等比数列的通项问题.
证法3:用待定系数法
设 , 即:
, 即: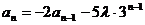 ,
,
比较系数得: ,所以
,所以 
 所以
所以 ,
,
所以数列 是公比为-2,首项为
是公比为-2,首项为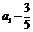 的等比数列.
的等比数列.
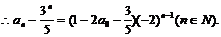 即
即  .
.
方法4:本题也可用数学归纳法证.
(i)当n=1时,由已知a1=1-2a0,等式成立;
( ii)假设当n=k(k≥1)等式成立,则
那么

也就是说,当n=k+1时,等式也成立. 根据(i)和(ii),可知等式对任何n∈N,成立.
规律: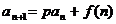 类型共同的规律为:两边同除以
类型共同的规律为:两边同除以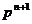 ,累加求和,只是求和的方法不同.
,累加求和,只是求和的方法不同.
5.形如 ,其中
,其中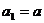 )型
)型
(1)若c=1时,数列{ }为等差数列;
}为等差数列;
(2)若d=0时,数列{ }为等比数列;
}为等比数列;
(3)若 时,数列{
时,数列{ }为线性递推数列,其通项可通过待定系数法构造辅助数列来求.
}为线性递推数列,其通项可通过待定系数法构造辅助数列来求.
方法如下:设 ,
,
得 ,与题设
,与题设 比较系数得
比较系数得
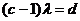 ,所以
,所以
所以有:
因此数列 构成以
构成以 为首项,以c为公比的等比数列,
为首项,以c为公比的等比数列,
所以 
即: .
.
规律:将递推关系 化为
化为 ,构造成公比为c的等比数列
,构造成公比为c的等比数列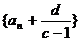 从而求得通项公式
从而求得通项公式
有时我们从递推关系 中把n换成n-1有
中把n换成n-1有 ,两式相减有
,两式相减有 从而化为公比为c的等比数列
从而化为公比为c的等比数列 ,进而求得通项公式.
,进而求得通项公式.  ,再利用类型(1)即可求得通项公式.我们看到此方法比较复杂.
,再利用类型(1)即可求得通项公式.我们看到此方法比较复杂.
例1.已知数列 中,
中, 求通项
求通项 .
.
分析:两边直接加上 ,构造新的等比数列。
,构造新的等比数列。
解:由 得
得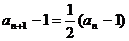 ,
,
所以数列 构成以
构成以 为首项,以
为首项,以 为公比的等比数列
为公比的等比数列
所以 ,即
,即
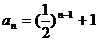 .
.
方法二:由 

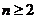 时,
时,
两式相减得 

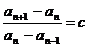 ,
,
数列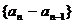 是以
是以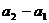 =
=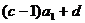 为首项,以c为公比的等比数列.
为首项,以c为公比的等比数列.


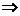

=(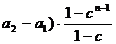

 .
.
方法三:迭代法
由 递推式
直接迭代得
= =
=
= .
.
方法四:归纳、猜想、证明.
先计算出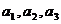 ,再猜想出通项
,再猜想出通项 ,最后用数学归纳法证明.
,最后用数学归纳法证明.
注:请用这三种方法来解例题,体会并比较它们的不同.
4.形如 型
型
(1)若 (p为常数),则数列{
(p为常数),则数列{ }为“等积数列”,它是一个周期数列,周期为2,其通项分奇数项和偶数项来讨论;
}为“等积数列”,它是一个周期数列,周期为2,其通项分奇数项和偶数项来讨论;
(2)若f(n)为n的函数(非常数)时,可通过逐差法得 ,两式相除后,分奇偶项来分求通项.
,两式相除后,分奇偶项来分求通项.
例1. 已知数列
 ,求此数列的通项公式.
,求此数列的通项公式.
注:同上例类似,略.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com