
2、 A、B两质点以相同的水平速度υ0抛出,A在竖直平面内运动,落地点为P1,B沿光滑 斜面运动,落地点为P2,不计阻力,如左下图所示,比较P1、P2在x轴上的远近关系是( )
斜面运动,落地点为P2,不计阻力,如左下图所示,比较P1、P2在x轴上的远近关系是( )
A、P1较远 B、P2较远
C、P1、P2等远 D 、A、B两项都有可能
1、一个小球在竖直放置的光滑圆环的内槽里作圆周运动,则关于小球加速度方向正确的是( )
A、一定指向圆心 B、一定不指向圆心
C、只在最高点和最低点时指向圆心 D、不能确定是否指向圆心
20.(本题满分14分)某企业为了适应市场需求,计划从2010年元月起,在每月固定投资5万元的基础上,元月份追加投资6万元,以后每月的追加投资额均为之前几个月投资额总和的20%,但每月追加部分最高限额为10万元. 记第n个月的投资额为
(1)求 与n的关系式;
与n的关系式;
(2)预计2010年全年共需投资多少万元?(精确到0.01,参考数据: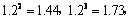
贵州省兴义市第九中学2010届高三第一次月考
19.(本小题满分14分)
通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设 表示学生注意力随时间
表示学生注意力随时间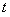 (分钟)的变化规律(
(分钟)的变化规律( 越大,表明学生注意力越集中),经过实验分析得知:
越大,表明学生注意力越集中),经过实验分析得知:
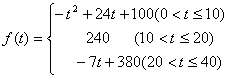
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
18.(本小题满分14分)
已 知a>0,函数 在x
在x
 是一个单调函数,
是一个单调函数,
(1)求实数a的取值范围;
(2)设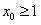 ,
, ,且
,且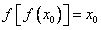 ,试证明:
,试证明:
17.(本小题满分14分)
设函数 ,
,
(1)判断函数 的奇偶性;
的奇偶性;
(2)求函数的最小值.
16.(本题满分12分)
已知函数  和
和 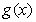 =
= 
 2 + 8
2 + 8 (
( 为常数)的图象在
为常数)的图象在
 = 3 处有平行切线.
= 3 处有平行切线.
(1)求
 的值;
的值;
(2)求函数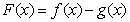 的极大值和极小值.
的极大值和极小值.
15.(本小题满分12分)
现有一批产品共有 件,其中
件,其中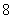 件为正品,
件为正品,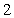 件为次品:
件为次品:
(Ⅰ)如果从中取出一件,然后放回,再取一件,求连续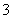 次取出的都是正品的概率;
次取出的都是正品的概率;
(Ⅱ)如果从中一次取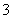 件,求
件,求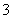 件都是正品的概率
件都是正品的概率
14.函数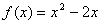 ,
,
 图象上的最高点为A,最低点为B,A、B两点之间的距离是
图象上的最高点为A,最低点为B,A、B两点之间的距离是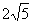 ,则实数
,则实数 的取值范围是_______
的取值范围是_______
13.已知定义在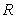 上的奇函数
上的奇函数 的图象关于直线
的图象关于直线 对称,
对称,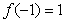 ,则
,则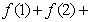
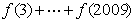 的值为________
的值为________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com