2.　 若函数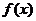 是定义在R上的偶函数，在 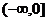上是减函数，且 ，则使得的取值范围是　　 (　　 )

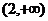　　 A. 　 　B. 　　 C. 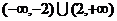　D.(－2，2)

1.某学生离家去学校，由于怕迟到，所以一开始就跑步，等跑累了，再走余下的路，下图中y轴表示离学校的距离，x轴表示出发后的时间，则适合题意的图形是(　　 )

[例1]判断函数的单调性.

错解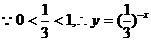：是减函数

错因：概念不清，导致判断错误.这是一个复合函数，而复合函数的单调性(或单调区间)，仍是从基础函数的单调性(或单调区间)分析，但需注意内函数与外函数的单调性的变化.当然这个函数可化为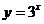，从而可判断出其单调性.

正解：　令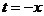，则该函数在R上是减函数，又在R上是减函数，

∴　是增函数

[例2]判断函数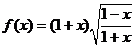的奇偶性.

错解：∵＝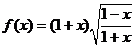

　∴

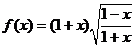　∴是偶函数

错因：对函数奇偶性定义实质理解不全面.对定义域内任意一个x，都有f(-x)=f(x)，f(-x)=-f(x)的实质是：函数的定义域关于原点对称.这是函数具备奇偶性的必要条件.

正解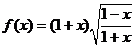：有意义时必须满足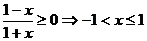

即函数的定义域是{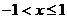｜}，由于定义域不关于原点对称，所以该函数既不是奇函数也不是偶函数

[例3] 判断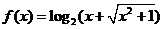的奇偶性.

错解：∵

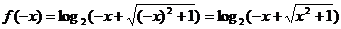
　　∴且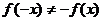

　　所以该函数既不是奇函数也不是偶函数

错因：对数运算公式不熟悉，或者说奇偶性的判别方法不灵活.定义中f(-x)=-f(x)

f(-x)=f(x)，也可改为研究f(-x)+f(x) =0 ，f(-x)-f(x)＝0是否成立.

正解：方法一：∵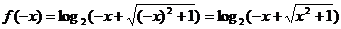

＝＝＝－

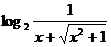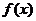
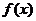∴是奇函数

　方法二：∵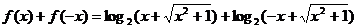

＝

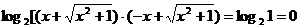
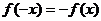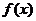　∴是奇函数

[例4]函数y=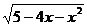的单调增区间是_________.

错解：因为函数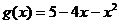的对称轴是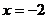，图像是抛物线，开口向下，由图可知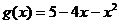在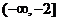上是增函数，所以y=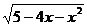的增区间是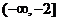

错因：在求单调性的过程中注意到了复合函数的单调性研究方法，但没有考虑到函数的单调性只能在函数的定义域内来讨论，从而忽视了函数的定义域，导致了解题的错误.

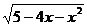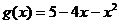正解：y=的定义域是，又在区间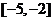上增函数，在区间是减函数，所以y=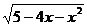的增区间是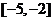

[例5] 已知奇函数f(x)是定义在(－3，3)上的减函数，且满足不等式f(x－3)+f(x²－3)<0,求x的取值范围.

错解：∵f(x)是奇函数，∴f(x－3)<－f(x²－3)=　f (3－x²),又f(x)在(－3，3)上是减函数，

∴x－3>3－x²,即x²+x－6>0

解得x>2或x<－3

又 f(x)是定义在(－3，3)上的函数，

所以2＜x＜3

错因：只考虑到奇函数与单调性，而没有正确理解函数的定义域.

正解：由,故0<x<,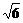

又∵f(x)是奇函数，∴f(x－3)<－f(x²－3)=f(3－x²),又f(x)在(－3，3)上是减函数，

∴x－3>3－x²,即x²+x－6>0,解得x>2或x<－3,综上得2<x<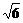,即A={x|2<x<},

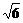[例6] 作出下列函数的图像(1)y=|x-2|(x+1)；(2).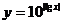

分析：显然直接用已知函数的解析式列表描点有些困难，除去对其函数性质分析外，我们还应想到对已知解析式进行等价变形.在变换函数解析式中运用了转化变换和分类讨论的思想.

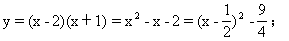解：(1)当x≥2时，即x-2≥0时，

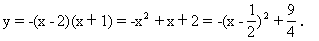当x＜2时，即x-2＜0时，

所以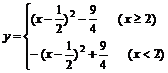

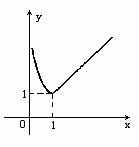这是分段函数，每段函数图像可根据二次函数图像作出(见图)

(2)当x≥1时，lgx≥0，y=10lgx=x；

当0＜x＜1时，lgx＜0，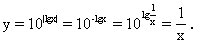

所以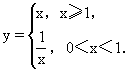

这是分段函数，每段函数可根据正比例函数或反比例函数作出.(见图)

点评：作不熟悉的函数图像，可以变形成基本函数再作图，但要注意变形过程是否等价，要特别注意x，y的变化范围.因此必须熟记基本函数的图像.例如：一次函数、反比例函数、二次函数、指数函数、对数函数，及三角函数、反三角函数的图像.

[例7]若f(x)= 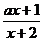在区间(－2，+)上是增函数，求a的取值范围

解：设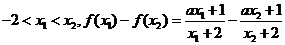

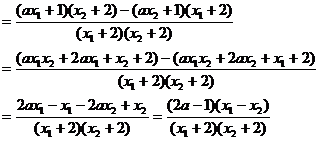
　　由f(x)=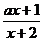在区间(－2，+)上是增函数得

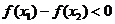
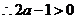　∴a＞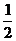

点评：有关于单调性的问题，当我们感觉陌生，不熟悉或走投无路时，回到单调性的定义上去，往往给我们带来“柳暗花明又一村”的感觉.

[例8] 已知函数f(x)在(－1，1)上有定义，f(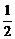)=－1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(－1,1)都有f(x)+f(y)=f(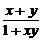),试证明：

(1)f(x)为奇函数；(2)f(x)在(－1，1)上单调递减

解：证明：(1)由f(x)+f(y)=f(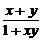),令x=y=0,得f(0)=0,令y=－x,得f(x)+f(－x)=f(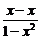)=f(0)=0.∴f(x)=－f(－x).∴f(x)为奇函数.

(2)先证f(x)在(0，1)上单调递减.

令0<x₁<x₂<1,则f(x₂)－f(x₁)=f(x₂)+f(－x₁)=f()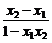

∵0<x₁<x₂<1,∴x₂－x₁>0,1－x₁x₂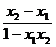>0，∴>0,

又(x₂－x₁)－(1－x₂x₁)=(x₂－1)(x₁+1)<0

∴x₂－x₁<1－x₂x₁,

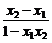∴0<<1,由题意知f()<0，?

即f(x₂)<f(x₁).

∴f(x)在(0，1)上为减函数，又f(x)为奇函数且f(0)=0.

∴f(x)在(－1，1)上为减函数.

点评：本题知识依托：奇偶性及单调性定义及判定、赋值法及转化思想.对函数的奇偶性、单调性的判定以及运算能力和逻辑推理能力要求较高. 如果“赋值”不够准确，运算技能不过关，结果很难获得. 对于(1)，获得f(0)的值进而取x=－y是解题关键；对于(2)，判定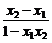的范围是解题的焦点.

3. 用列表描点法总能作出函数的图像，但是不了解函数本身的特点，就无法了解函数图像的特点，如二次函数图像是抛物线，如果不知道抛物线的顶点坐标和存在着对称轴，盲目地列表描点是很难将图像的特征描绘出来的.

2.对函数奇偶性定义的理解，不能只停留在f(-x)=f(x)和f(-x)=-f(x)这两个等式上，要明确对定义域内任意一个x，都有f(-x)=f(x)，f(-x)=-f(x)的实质：函数的定义域关于原点对称.这是函数具备奇偶性的必要条件.稍加推广，可得函数f(x)的图像关于直线x=a对称的充要条件是对定义域内的任意x，都有f(x+a)=f(a-x)成立.函数的奇偶性是其相应图像的特殊的对称性的反映.

这部分的难点是函数的单调性和奇偶性的综合运用.根据已知条件，调动相关知识，选择恰当的方法解决问题，是对学生能力的较高要求.

1. 对函数单调性的理解， 函数的单调性一般在函数的定义域内的某个子区间上来讨论，函数y=f(x)在给定区间上的单调性，反映了函数在区间上函数值的变化趋势，是函数在区间上的整体性质，但不一定是函数在定义域上的整体性质.函数的单调性是对某个区间而言的，所以要受到区间的限制.

3.函数的图像：将自变量的一个值x₀作为横坐标，相应的函数值f(x₀)作为纵坐标，就得到平面内的一个点(x₀,f(x₀))，当自变量取遍函数定义域内的每一个值时，就得到一系列这样的点，所有这些点的集合(点集)组成的图形就是函数y=f(x)的图像.

2.函数的奇偶性：

　(1)奇函数：一般地，如果对于函数f(x)的定义域内的任意一个x，都有f(－x) =－f(x)，那么函数f(x)就叫做奇函数.

　(2)一般地，如果对于函数f(x)的定义域内的任意一个x，都有f(－x) =f(x)，那么函数f(x)就叫做偶函数.

　(3)如果函数f(x)是奇函数或偶函数，那么就说f(x)具有奇偶性.

1.函数的单调性：

　(1)增函数：一般地，设函数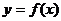的定义域为I，如果定义域I内某个区间上任意两个自变量的值x₁,x₂,当x₁＜x₂时，都有f(x₁)<f(x₂),那么就说f(x)在这个区间上是增函数.

　(2)减函数：一般地，设函数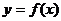的定义域为I，如果定义域I内某个区间上任意两个自变量的值x₁,x₂,当x₁＜x₂时,都有f(x₁)＞f(x₂),那么就说f(x)在这个区间上是减函数.

　(3)单调性(单调区间)如y=f(x)在某个区间上是增函数或减函数，那么就说函数f(x)在这区间上具有单调性，这一区间叫做函数y=f(x)的单调区间.

8.已知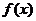函数是函数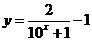(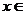R)的反函数，函数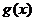的图像与函数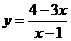的图像关于直线y＝x－1成轴对称图形，记＝+.

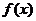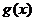(1)求函数F(x)的解析式及定义域；

(2)试问在函数F(x)的图像上是否存在两个不同的点A、B，使直线AB恰好与y轴垂直？若存在，求出A、B两点的坐标；若不存在，说明理由.

§2. 函数的性质