
5、图中曲线是幂函数y=xn在第一象限的图像,已知n可取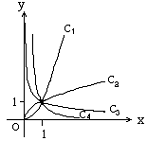 ±2,±
±2,±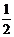 四个值,则相应于曲线c1、c2、c3、c4的n依次为( )
四个值,则相应于曲线c1、c2、c3、c4的n依次为( )
A.-2,-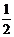 ,
,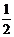 ,2
B.2,
,2
B.2,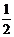 ,-
,-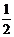 ,-2
,-2
C. -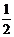 ,-2,2,
,-2,2,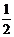 D. 2,
D. 2,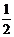 ,-2, -
,-2, -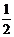
4、函数f(x)与g(x)=(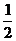 )x的图像关于直线y=x对称,则f(4-x2)的单调递增区间是 ( )
)x的图像关于直线y=x对称,则f(4-x2)的单调递增区间是 ( )
A. B.
B.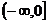 C.
C.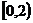 D.
D.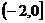
3、方程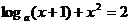 (0<a<1)的解的个数为( )
(0<a<1)的解的个数为( )
A.0 B.1 C.2 D.3
2、已知2lg(x-2y)=lgx+lgy,则 的值为( )
的值为( )
A.1 B.4 C.1或4 D.4 或 8
1. 函数
函数 的图像如图,其中a、b为常数,则下列结论正确的是( )
的图像如图,其中a、b为常数,则下列结论正确的是( )
A.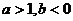 B.
B.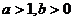
C.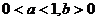 D.
D.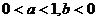
[例1]已知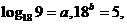 求
求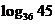
错解:∵ ∴
∴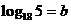
∴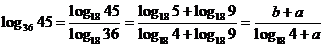
错因:因对性质不熟而导致题目没解完.
正解:∵ ∴
∴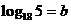
∴
[例2]分析方程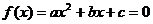 (
(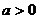 )的两个根都大于1的充要条件.
)的两个根都大于1的充要条件.
错解:由于方程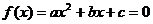 (
(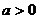 )对应的二次函数为
)对应的二次函数为
 的图像与x轴交点的横坐标都大于1即可.
的图像与x轴交点的横坐标都大于1即可.
故需满足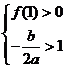 ,所以充要条件是
,所以充要条件是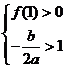
错因:上述解法中,只考虑到二次函数与x轴交点坐标要大于1,却忽视了最基本的的前题条件,应让二次函数图像与x轴有交点才行,即满足△≥0,故上述解法得到的不是充要条件,而是必要不充分条件.
正解:充要条件是
[例3]求函数 的单调区间.
的单调区间.
错解:令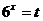 ,则
,则 =
=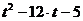
∴当t≥6,即x≥1时,y为关于t的增函数,
当t≤6,即x≤1时,y为关于t的减函数
∴函数 的单调递减区间是
的单调递减区间是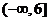 ,单调递增区间为
,单调递增区间为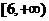
错因:本题为复合函数,该解法未考虑中间变量的取值范围.
正解:令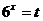 ,则
,则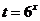 为增函数,
为增函数,
 =
=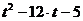 =
=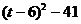
∴当t≥6,即x≥1时,y为关于t的增函数,
当t≤6,即x≤1时,y为关于t的减函数
∴函数 的单调递减区间是
的单调递减区间是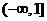 ,单调递增区间为
,单调递增区间为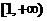
[例4]已知 在[0,1]上是
在[0,1]上是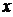 的减函数,则
的减函数,则 的取值范围是
的取值范围是
错解:∵ 是由
是由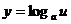 ,
, 复合而成,又
复合而成,又 >0
>0
∴ 在[0,1]上是
在[0,1]上是 的减函数,由复合函数关系知
的减函数,由复合函数关系知
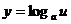 应为增函数,∴
应为增函数,∴ >1
>1
错因:错因:解题中虽然考虑了对数函数与一次函数复合关系,却忽视了数定义域的限制,单调区间应是定义域的某个子区间,即函数应在[0,1]上有意义.
正解:∵ 是由
是由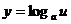 ,
, 复合而成,又
复合而成,又 >0
>0
∴ 在[0,1]上是
在[0,1]上是 的减函数,由复合函数关系知
的减函数,由复合函数关系知
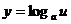 应为增函数,∴
应为增函数,∴ >1
>1
又由于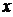 在[0,1]上时
在[0,1]上时  有意义,
有意义, 又是减函数,∴
又是减函数,∴ =1时,
=1时, 取最小值是
取最小值是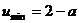 >0即可, ∴
>0即可, ∴ <2
<2
综上可知所求的取值范围是1< <2
<2
[例5]已知函数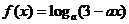 .
.
(1)当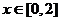 时
时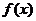 恒有意义,求实数
恒有意义,求实数 的取值范围.
的取值范围.
(2)是否存在这样的实数 使得函数
使得函数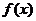 在区间[1,2]上为减函数,并且最大值为1,如果存在,试求出
在区间[1,2]上为减函数,并且最大值为1,如果存在,试求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
分析:函数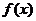 为复合函数,且含参数,要结合对数函数的性质具体分析找到正确的解题思路,是否存在性问题,分析时一般先假设存在后再证明.
为复合函数,且含参数,要结合对数函数的性质具体分析找到正确的解题思路,是否存在性问题,分析时一般先假设存在后再证明.
解:(1)由假设, >0,对一切
>0,对一切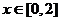 恒成立,
恒成立,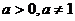
显然,函数g(x)=  在[0,2]上为减函数,从而g(2)=
在[0,2]上为减函数,从而g(2)=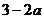 >0得到
>0得到 <
<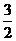
∴ 的取值范围是(0,1)∪(1,
的取值范围是(0,1)∪(1,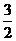 )
)
(2)假设存在这样的实数 ,由题设知
,由题设知 ,即
,即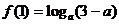 =1
=1
∴ =
=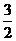 此时
此时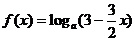
当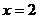 时,
时,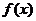 没有意义,故这样的实数不存在.
没有意义,故这样的实数不存在.
点评:本题为探索性问题,应用函数、方程、不等式之间的相互转化,存在性问题一般的处理方法是先假设存在,结合已知条件进行推理和等价转化,若推出矛盾,说明假设不成立.即不存在,反之没有矛盾,则问题解决.
[例6]已知函数f(x)= , 其中
, 其中 为常数,若当x∈(-∞, 1]时, f(x)有意义,求实数a的取值范围.
为常数,若当x∈(-∞, 1]时, f(x)有意义,求实数a的取值范围.
分析:参数深含在一个复杂的复合函数的表达式中,欲直接建立关于 的不等式(组)非常困难,故应转换思维角度,设法从原式中把
的不等式(组)非常困难,故应转换思维角度,设法从原式中把 分离出来,重新认识
分离出来,重新认识 与其它变元(x)的依存关系,利用新的函数关系,常可使原问题“柳暗花明”.
与其它变元(x)的依存关系,利用新的函数关系,常可使原问题“柳暗花明”.
解: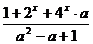 >0, 且a2-a+1=(a-
>0, 且a2-a+1=(a-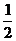 )2+
)2+ >0,
>0,
∴ 1+2x+4x·a>0, a>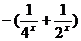 ,
,
当x∈(-∞, 1]时, y=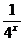 与y=
与y=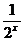 都是减函数,
都是减函数,
∴ y=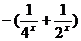 在(-∞, 1]上是增函数,
在(-∞, 1]上是增函数,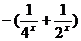 max=-
max=- ,
,
∴ a>- , 故a的取值范围是(-
, 故a的取值范围是(- , +∞).
, +∞).
点评:发掘、提炼多变元问题中变元间的相互依存、相互制约的关系、反客为主,主客换位,创设新的函数,并利用新函数的性质创造性地使原问题获解,是解题人思维品质高的表现.本题主客换位后,利用新建函数y=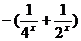 的单调性转换为函数最值巧妙地求出了实数a的取值范围.此法也叫主元法.
的单调性转换为函数最值巧妙地求出了实数a的取值范围.此法也叫主元法.
[例7]若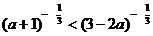 ,试求
,试求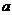 的取值范围.
的取值范围.
解:∵幂函数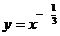 有两个单调区间,
有两个单调区间,
∴根据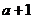 和
和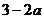 的正、负情况,有以下关系
的正、负情况,有以下关系
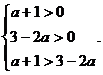 ①
① 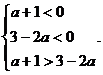 ②
② 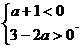 ③
③
解三个不等式组:①得 <
<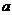 <
<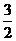 ,②无解,③
,②无解,③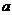 <-1
<-1
∴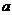 的取值范围是(-∞,-1)∪(
的取值范围是(-∞,-1)∪( ,
,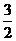 )
)
点评:幂函数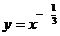 有两个单调区间,在本题中相当重要,不少学生可能在解题中误认为
有两个单调区间,在本题中相当重要,不少学生可能在解题中误认为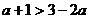 ,从而导致解题错误.
,从而导致解题错误.
[例8] 已知a>0 且a≠1 ,f (log a x ) =  (x -
(x -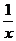 )
)
(1)求f(x);
(2)判断f(x)的奇偶性与单调性;
(3)对于f(x) ,当x ∈(-1 , 1)时 , 有f( 1-m ) +f (1- m2 ) < 0 ,求m的集合M .
分析:先用换元法求出f(x)的表达式;再利用有关函数的性质判断其奇偶性和单调性;然后利用以上结论解第三问.
解:(1)令t=logax(t∈R),则
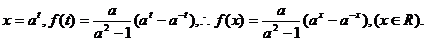
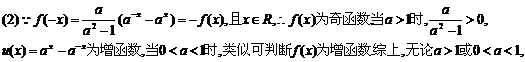
f(x)在R上都是增函数.


点评:对含字母指数的单调性,要对字母进行讨论.对本例的③不需要代入f(x)的表达式可求出m的取值范围,请同学们细心体会.
6.幂函数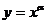 的性质,要注意
的性质,要注意 的取值变化对函数性质的影响.
的取值变化对函数性质的影响.
(1)当 时,幂函数是奇函数;(2)当
时,幂函数是奇函数;(2)当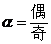 时,幂函数是偶函数;(3)当
时,幂函数是偶函数;(3)当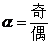 时,定义域不关于原点对称,幂函数为非奇非偶函数.
时,定义域不关于原点对称,幂函数为非奇非偶函数.
5.对数函数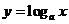
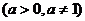 与指数函数
与指数函数
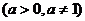 互为反函数,会将指数式与对数式相互转化.
互为反函数,会将指数式与对数式相互转化.
4.函数 的研究方法一般是先研究
的研究方法一般是先研究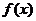 的性质,再由
的性质,再由 的情况讨论
的情况讨论 的性质.
的性质.
3.利用指数函数的性质解题,一定要注意底数的取值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com