
2、下列物质能与二氧化硅起化学反应的是( )
①浓硝酸 ②水 ③王水 ④氢氧酸 ⑤KOH溶液
A.①② B.②④ C.④⑤ D.③⑤
1、2008年9月27日16时41分,航天员翟志刚身着“飞天”航天服出舱活动,茫茫太空中第一次留下中国人的足迹。“飞天”舱外航天服是我国自行研制的,使用了多种新材料。下列对材料的说法错误的是( )
A.新材料的开发和应用,是社会发展和人类进步的一种标志
B.水泥、玻璃、陶瓷属于新型无机非金属材料
C.传统的无机非金属材料虽有不少优点,但质脆、经不起热冲击
D.新型结构陶瓷具有承受高温、抗氧化、耐磨损、密度小等特点,可应用于宇航事业
7.
2000年某内河可供船只航行的河流段长为1000千米,由于水资源的过度使用,促使河水断流。从2000起该内河每年船只可行驶的河段长度仅为上一年的 ,则到2009年,该内河可供船只行驶的河段长度为___________
,则到2009年,该内河可供船只行驶的河段长度为___________
答:
三角函数专题
第一课时
例1.
解:


例2.
解:
 ,
,
 。
。
例3.
解:


例4.
解:



备用题1.
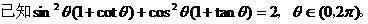 求
求 的值。
的值。
解:由 得
得
 即
即

两边同时除以 得
得 ,
, 。
。
(本题也可以进行切割化弦,进而求 的值。)
的值。)
备用题2.


解:由题设知,
 ,
,
由求根公式,





作业1.
解:
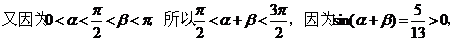


作业2.
解:

作业3.

解:
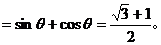
作业4.
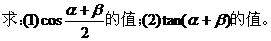
解:(1)因为

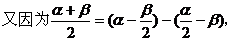


(2)


第二课时
例1.已知 且
且 为锐角,试求
为锐角,试求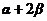 的值。
的值。
解: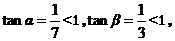 且
且 为锐角,所以
为锐角,所以

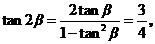
 ,所以
,所以 。
。
例2.求证: 。
。
证明:左边=

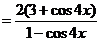 =右边,原式得证。
=右边,原式得证。
例3.求函数 的值域。
的值域。
解:设 ,则原函数可化为
,则原函数可化为
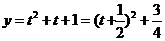 ,因为
,因为 ,所以
,所以
当 时,
时, ,当
,当 时,
时, ,
,
所以,函数的值域为 。
。
例4.已知 的最大值为3,最小值为-1,求
的最大值为3,最小值为-1,求 的值。
的值。
解:当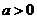 时,由
时,由 ,当
,当 时,由
时,由 ,
,
所以, 。
。
备用题1.已知 求
求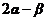 的值。
的值。
解: ,
,
又 ,
, ,
,
而 ,
, 所以
所以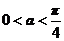 ,所以
,所以 。
。
备用题2.已知 求证:
求证: 。
。
证明: 所以
所以

所以,

又 所以
所以 。
。
作业1.已知 都是锐角,且
都是锐角,且 求
求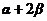 。
。
解:由题意,
所以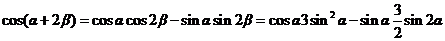
 ,又因为
,又因为 都是锐角,所以
都是锐角,所以 ,
,
所以, 。(也可以用
。(也可以用 、
、 来求)
来求)
作业2.求函数 的值域。
的值域。
解:设 ,则
,则 ,
,
原函数可化为
当t=1时, ,当
,当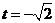 时,
时, ,所以,函数值域为
,所以,函数值域为 。
。
作业3.求函数 的最大值与最小值。
的最大值与最小值。
解: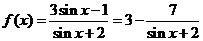 ,当
,当 时,
时, ,
,
当 时,
时, 。
。
作业4.求证: 。
。
证明: 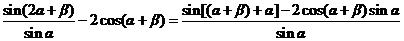
 ,
,
所以,左边=右边,原式得证。
第三课时
例1.求函数 的最小值,并求其单调区间。
的最小值,并求其单调区间。
解:

因为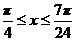 ,所以
,所以 ,所以
,所以 ,
,
所以,当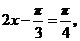 即
即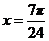 时,
时, 的最小值为
的最小值为 ,
,
因为 是单调递增的,所以
是单调递增的,所以 上单调递增。
上单调递增。
例2.已知函数 。
。
(1) 求 的最小正周期、
的最小正周期、 的最大值及此时x的集合;
的最大值及此时x的集合;
(2) 证明:函数 的图像关于直线
的图像关于直线 对称。
对称。
解:

(1)所以 的最小正周期
的最小正周期 ,因为
,因为 ,
,
所以,当 ,即
,即 时,
时, 最大值为
最大值为 ;
;
(2)证明:欲证明函数 的图像关于直线
的图像关于直线 对称,只要证明对任意
对称,只要证明对任意 ,有
,有 成立,
成立,
因为 ,
,
 ,
,
所以 成立,从而函数
成立,从而函数 的图像关于直线
的图像关于直线 对称。
对称。
例3.已知函数 ,若
,若 ,且
,且 ,求
,求 的取值范围。
的取值范围。
解: ,因为
,因为 ,所以
,所以 ,所以
,所以 ,
,
所以 ,而
,而 ,即
,即 ,
,
所以, ,解得:
,解得: ,所以
,所以 的取值范围是
的取值范围是 。
。
例4.已知函数 。
。
(1) 求 的最小正周期;
的最小正周期;
(2) 求 的最小值及取得最小值时相应的x值;
的最小值及取得最小值时相应的x值;
(3) 若当 时,求
时,求 的值。
的值。
解:


(1) 由上可知, 得最小正周期为
得最小正周期为 ;
;
(2) 当 ,即
,即 时,
时, 得最小值为-2;
得最小值为-2;
(3) 因为 ,所以
,所以 ,令
,令 ,
,
所以 ,所以
,所以 。
。
备用题1.已知函数 。
。
(1) 将 写成含
写成含 的形式,并求其对称中心;
的形式,并求其对称中心;
(2) 如果三角形ABC的三边a、b、c满足b2=ac,且边b所对角为x,试求x的范围及此时函数 的值域。
的值域。
解:(1)  ,
,
令 得
得 ,即对称中心为
,即对称中心为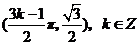
(2)由b2=ac, ,所以
,所以 ,此时
,此时 ,所以
,所以 ,
,
所以 ,即
,即 值域为
值域为 。
。
备用题2.已知函数 ,求
,求
(1) 当x为何值时,函数有最大值?最大值为多少?
(2) 求将函数的图像按向量 平移后得到的函数解析式,并判断平移后函数的奇偶性。
平移后得到的函数解析式,并判断平移后函数的奇偶性。
解:(1) ,
,
当 ,即
,即 时,
时, ;
;
(2)按 平移,即将函数
平移,即将函数 的图像向左平移
的图像向左平移 单位,再向下平移2个单位得到所求函数的图像,所以得到解析式为
单位,再向下平移2个单位得到所求函数的图像,所以得到解析式为
 ,
,
由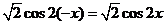 ,所以平移后函数为偶函数。
,所以平移后函数为偶函数。
作业1.已知函数 的最小正周期为
的最小正周期为 ,且当
,且当 时,函数有最小值,(1)求
时,函数有最小值,(1)求 的解析式;(2)求
的解析式;(2)求 的单调递增区间。
的单调递增区间。
解:(1)
 ,由题意
,由题意 ,
,
当 时,
时, ,
, ,不是最小值。
,不是最小值。
当 时,
时, ,
, ,是最小值。
,是最小值。
所以 ;
;
(2)当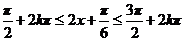 ,
,
即 时,函数单调递增。
时,函数单调递增。
作业2.已知定义在R上的函数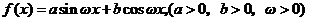 的最小正周期为
的最小正周期为 ,
, ,
, 。(1)写出函数
。(1)写出函数 的解析式;(2)写出函数
的解析式;(2)写出函数 的单调递增区间;(3)说明
的单调递增区间;(3)说明 的图像如何由函数
的图像如何由函数 的图像变换而来。
的图像变换而来。
解:(1)  ,由题意,
,由题意,
 ,代入
,代入 ,有
,有 ,所以
,所以 ;
;
(2) 当 ,函数单调增;
,函数单调增;
(3) 将函数 的图像向左平移
的图像向左平移 单位,再将得到的函数图像上所有的点的纵坐标不变,横坐标缩短到原来的
单位,再将得到的函数图像上所有的点的纵坐标不变,横坐标缩短到原来的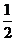 倍,可得到函数
倍,可得到函数 的图像。
的图像。
作业3.已知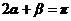 ,求
,求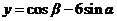 的最值。
的最值。
解:因为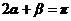 ,即
,即 ,原函数化为
,原函数化为
 ,
,
当 时,
时, ,当
,当 时,
时, 。
。
作业4.就三角函数 的性质,除定义域外,请再写出三条。
的性质,除定义域外,请再写出三条。
解:
a. 奇偶性:非奇非偶函数;
b.
单调性:在 上为单调增函数,
上为单调增函数,
在 上为单调减函数;
上为单调减函数;
c.
周期性:最小正周期 ;
;
d.
值域与最值:值域 ,当
,当 时,
时, 取最小值
取最小值 ,
,
当 时,
时, 取最大值
取最大值 ;
;
e.对称性:对称轴 ,对称中心
,对称中心 。
。
第四课时
例1.在 中,角A、B、C满足的方程
中,角A、B、C满足的方程 的两根之和为两根之积的一半,试判断
的两根之和为两根之积的一半,试判断 的形状。
的形状。
解:由条件可知, ,即
,即 ,因为
,因为 ,所以
,所以 ,即
,即 ,所以
,所以 ,所以A=B,即
,所以A=B,即 为等腰三角形。
为等腰三角形。
例2.在 中,a、b、c分别是角A、B、C的对边,若
中,a、b、c分别是角A、B、C的对边,若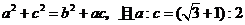 ,求角C的值。
,求角C的值。
解: ,所以
,所以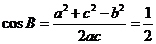 ,所以
,所以 ,所以
,所以 ,又
,又 ,所以
,所以 ,即
,即 ,
,
得 ,所以
,所以 。
。
例3.在 中,a、b、c分别是角A、B、C的对边,且
中,a、b、c分别是角A、B、C的对边,且 ,
,
(1)求 的值;
的值;
(2)若 ,且a=c,求
,且a=c,求 的面积。
的面积。
解:(1)由正弦定理及 ,有
,有 ,
,
即 ,所以
,所以 ,
,
又因为 ,
, ,所以
,所以 ,因为
,因为 ,所以
,所以 ,又
,又 ,所以
,所以 。
。
(2)在 中,由余弦定理可得
中,由余弦定理可得 ,又
,又 ,
,
所以有 ,所以
,所以 的面积为
的面积为
 。
。
例4.在 中,A、B、C满足
中,A、B、C满足 ,求
,求 的值。
的值。
解:由 ,且
,且 ,所以
,所以 ,
,


 ,
,
所以 。
。
备用题1.在 中,A、B、C满足
中,A、B、C满足 ,
,
(1)用 表示
表示 ; (2)求角B的取值范围。
; (2)求角B的取值范围。
解:(1) 因为 ,所以
,所以 ,由
,由 ,
,
得 (1),易知
(1),易知 ,
,
若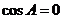 ,则
,则 ,所以
,所以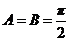 ,不合题意,
,不合题意,
若 ,则
,则 ,不合题意,
,不合题意,
对(1)式两边同除以 得,
得,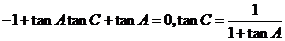 ;
;
(2)因为C为 的一个内角,所以
的一个内角,所以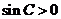 ,则由
,则由 ,
,
知 异号,若
异号,若 ,则A为钝角,B为锐角,此时
,则A为钝角,B为锐角,此时
 ,因为
,因为 ,不合题意;
,不合题意;
若 ,则B为钝角, A为锐角,
,则B为钝角, A为锐角,
则 ,因为A为锐角,所以
,因为A为锐角,所以 ,所以
,所以 ,所以
,所以 。
。
备用题2.已知A、B、C是 的三个内角,
的三个内角, ,若任意交换两个角的位置,y的值是否变化?证明你的结论。
,若任意交换两个角的位置,y的值是否变化?证明你的结论。
证明:因为A、B、C是 的三个内角,
的三个内角, ,所以
,所以 ,
,

 ,
,
因此任意交换两个角的位置,y的值不变。
作业1.在 中,a、b、c分别是角A、B、C的对边,且
中,a、b、c分别是角A、B、C的对边,且 ,
,
(1) 求角B的大小;(2)若 ,求a的值。
,求a的值。
解:(1)由正弦定理,条件 可化成
可化成 ,
,
即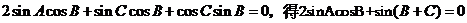 ,
,
因为 ,所以
,所以 ,所以
,所以 ,
,
因为 ,所以
,所以 ,B为三角形内角,所以
,B为三角形内角,所以 ;
;
(也可以用余弦定理进行角化边完成)
(2)将 ,
, 代入余弦定理
代入余弦定理 ,得
,得
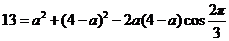 ,整理得
,整理得 ,解得
,解得 。
。
作业2.在 中,
中, ,且
,且 ,判断三角形形状。
,判断三角形形状。
解:因为 ,则
,则 ,则
,则 ,
,
又因为 ,所以
,所以 ,所以
,所以 ,若
,若 ,则
,则 ,
, 无意义,
无意义,
所以 ,三角形为正三角形。
,三角形为正三角形。
作业3.在 中,已知A、B、C成等差数列,求
中,已知A、B、C成等差数列,求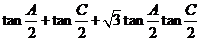 的值。
的值。
解:因为A、B、C成等差数列,则 ,所以
,所以
 。
。
作业4.在 中,
中, ,求
,求 的值和三角形
的值和三角形 面积。
面积。
解:由 ,因为
,因为 ,
,
所以 ,又因为
,又因为
 ,
,

第五课时
例1.已知向量 ,
,
(1)求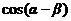 的值;(2)若
的值;(2)若 的值。
的值。
解:(1)因为
所以
又因为 ,所以
,所以 ,
,
即 ;
;
(2)  ,
,
又因为 ,所以
,所以  ,
,
 ,所以
,所以 ,所以
,所以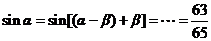 。
。
例2.已知向量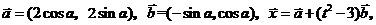
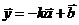 ,且
,且 ,
,
(1)求函数 的表达式;
的表达式;
(2)若 ,求
,求 的最大值与最小值。
的最大值与最小值。
解:(1) ,
, ,
, ,又
,又 ,
,
所以 ,
,
所以 ,即
,即 ;
;
(2)由(1)可得,令 导数
导数 ,解得
,解得 ,列表如下:
,列表如下:
|
t |
-1 |
(-1,1) |
1 |
(1,3) |
 导数 导数 |
0 |
- |
0 |
+ |
 |
极大值 |
递减 |
极小值 |
递增 |
而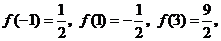 所以
所以 。
。
例3.已知向量 ,其中
,其中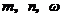 是常数,且
是常数,且 ,函数
,函数 的周期为
的周期为 ,当
,当 时,函数取得最大值1。
时,函数取得最大值1。
(1)求函数 的解析式; (2)写出
的解析式; (2)写出 的对称轴,并证明之。
的对称轴,并证明之。
解:(1)  ,
,
由周期为 且最大值为1,所以
且最大值为1,所以 由
由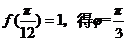 ,
,
所以 ;
;
(2)由(1)知,令 ,解得对称轴方成为
,解得对称轴方成为 ,
,
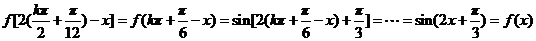 ,所以
,所以 是
是 的对称轴。
的对称轴。
例4.已知向量 ,定义函数
,定义函数 。
。
(1)求函数 的最小正周期;
的最小正周期;
(2)确定函数 的单调区间。
的单调区间。
解:(1) ,
,
所以 ,所以最小正周期为
,所以最小正周期为 ;
;
(2)令试题详情
6.某林场去年年底木材存量为 (立方米),若森林以每年25%的增长率生长,每年冬天要砍伐的木材量为
(立方米),若森林以每年25%的增长率生长,每年冬天要砍伐的木材量为 (立方米),设经过
(立方米),设经过 年林场木材的存量为
年林场木材的存量为
 ,则
,则 =_____________
=_____________
答:
5.从2001年到2004年间,王先生每年7月1日都到银行存入 元的一年定期储蓄,准备为孩子读大学用。若年利率为
元的一年定期储蓄,准备为孩子读大学用。若年利率为 (扣税后)保持不变,且每年到期的存款本息自动转为新的一年的定期,到2005年7月1日,其不再去银行存款,而将所有存款本息取回,则取回的总金额是______________
(扣税后)保持不变,且每年到期的存款本息自动转为新的一年的定期,到2005年7月1日,其不再去银行存款,而将所有存款本息取回,则取回的总金额是______________
答: 
4. 若数列
 是等差数列,则有数列
是等差数列,则有数列
 也为等差数列,类比上述性质,相应的,若数列
也为等差数列,类比上述性质,相应的,若数列 是等比数列,且
是等比数列,且
 ,则有
,则有 ____________
____________ 也是等比数列。
也是等比数列。
答:
3.将正奇数按下表排成5列
|
|
第1列 |
第2列 |
第3列 |
第4列 |
第5列 |
|
第1行 |
|
1 |
3 |
5 |
7 |
|
第2行 |
15 |
13 |
11 |
9 |
|
|
第3行 |
|
17 |
19 |
21 |
23 |
 |
 |
 |
 |
 |
 |
那么,2005应在第______行______列。
答: 251行第4列
2.如果 在
在 上的最大值是2,那么
上的最大值是2,那么 在
在 上的最小值是__________
上的最小值是__________
答:
1.定义符号函数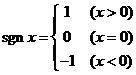 ,则不等式
,则不等式 的解集是________________
的解集是________________
答:
9.已知函数 的反函数为
的反函数为 (
(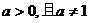 ),则函数
),则函数 的图象必过定点
. ( (1,0) )
的图象必过定点
. ( (1,0) )
10. 设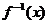 是函数f(x)=
是函数f(x)= 的反函数,则
的反函数,则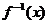 与
与 的大小关系是
. (
的大小关系是
. (  )
)
备用题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com