2．一个首项为正数的等差数列中，前3项的和等于前11项的和，当这个数列的前n项和最大时，n等于．　　　　　　　　　　　　　　　　　　　 　(　　 )

A．5　　　　 　B．6　　　 　　　　C．7　　　 　D．8

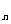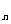1．设S和T分别为两个等差数列的前n项和，若对任意n∈N，

　　　　　　　　　　　　　　　　　 　 (　　 )

A．4∶3　　 　　　　B．3∶2　 　　　　C．7∶4　　 　　D．78∶71

8．通过解题后的反思，找准自己的问题，总结成功的经验，吸取失败的教训，增强解综合题的信心和勇气，提高分析问题和解决问题的能力．

数列是高中数学的重要内容，又是学习高等数学的基础，所以在高考中占有重要的地位。高考对本章的考查比较全面，等差数列，等比数列的考查每年都不会遗漏。解答题多为中等以上难度的试题，突出考查考生的思维能力，解决问题的能力，试题大多有较好的区分度。有关数列的试题经常是综合题，经常把数列知识和指数函数、对数函数和不等式的知识综合起来，试题也常把等差数列、等比数列，求极限和数学归纳法综合在一起。探索性问题是高考的热点，常在数列解答题中出现。本章中还蕴含着丰富的数学思想，在主观题中着重考查函数与方程、转化与化归、分类讨论等重要思想，以及配方法、换元法、待定系数法等基本数学方法。应用问题考查的重点是现实客观事物的数学化，常需构造数列模型，将现实问题转化为数学问题来解决。

7．解综合题的成败在于审清题目，弄懂来龙去脉，透过给定信息的表象，抓住问题的本质，揭示问题的内在联系和隐含条件，明确解题方向，形成解题策略．

6．数列极限的综合题形式多样，解题思路灵活，但万变不离其宗，就是离不开数列极限的概念和性质，离不开数学思想方法，只要能把握这两方面，就会迅速打通解题思路．

5．注意与之间关系的转化。如：

=　 　，　 =．

4．注意一些特殊数列的求和方法。

3．对于一般数列的问题常转化为等差、等比数列求解。

2．在解决等差数列或等比数列的相关问题时，“基本量法”是常用的方法，但有时灵活地运用性质，可使运算简便。