
2.运动的合成与分解;
知识方法·要点
1.曲线运动的特征与条件;
11.(05·上海·23)一水平放置的圆盘绕竖直固定轴转动,在圆盘上沿半径开有一条宽度为2 mm的均匀狭缝.将激
光器与传感器上下对准,使二者间连线与转轴平行,分别置于圆盘的上下两侧,且可以同步地沿圆盘半径方向
匀速移动,激光器连续向下发射激光束.在圆盘转动过程中,当狭缝经过激光器与传感器之间时,传感器接收到
一个激光信号,并将其输入计算机,经处理后画出相应图线.图 (a)为该装置示意图,图(b)为所接收的光信号
随时间变化的图线,横坐标表示时间,纵坐标表示接收到的激光信号强度,图中Δt1=1.0×10-3 s, Δt2=0.8×
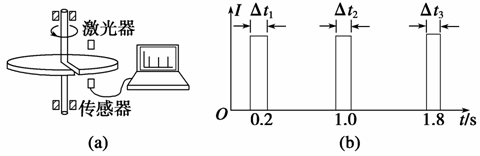 10-3 s.
10-3 s.
(1)利用图(b)中的数据求1 s时圆盘转动的角速度;
(2)说明激光器和传感器沿半径移动的方向;
(3)求图(b)中第三个激光信号的宽度Δt3;
答案 (1)7.85 rad/s (2)激光器和探测器沿半径由中心向边缘移动 (3)0.67×10-3 s
解析 (1)由图线读得,转盘的转动周期T =0.8 s ①
角速度ω= rad/s
=7.85 rad/s
②
rad/s
=7.85 rad/s
②
(2)激光器和传感器沿半径由中心向边缘移动(理由为:由于脉冲宽度在逐渐变窄,表明光信号能通过狭缝的时间逐渐减少,即圆盘上对应传感器所在位置的线速度逐渐增加,因此激光器和探测器半径由中心向边缘移动).
(3)设狭缝宽度为 d ,传感器接收到第 i个脉冲时距转轴的距离为 ri,第 i 个脉冲的宽度为Δti,激光器和传感器沿半径的运动速度为v.
?
Δti= ③
③
r3 - r 2 = r2 - r1 = vT ④
r2-r1=
r3-r2=
由以上各式解得

=0.67×10-3 s ⑤
10.(05·江苏·13)A、B两小球同时从距地面高为h=15 m处的同一点抛出,初速度大小均为v0=10 m/s,A球
直向下抛出,B球水平抛出,空气阻力不计,重力加速度取g=10 m/s2.求:
(1)A球经多长时间落地?
(2)A球落地时,A、B两球间的距离是多少?
答案 (1)1 s  (2)
(2)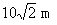
解析(1)A球做竖直下抛运动h=v0t+ gt2
gt2
将h=15 m,v0=10 m/s代入可得t=1 s?
(2)B球做平抛运动x=v0t,y= gt2
gt2
将v0=10 m/s、t=1 s代入,可得
x=10 m,y=5 m?
此时A球与B球的距离L=
将x、y、h数据代入得L=10 m
m
9.(04·全国卷Ⅱ·23)一水平放置的水管,距地面高h =1.8 m,管内横截面积S =2.0 cm2.有水从管口处以不变的速度v=2.0 m/s源源不断地沿水平方向射出,设出口处横截面上各处水的速度都相同,并假设水流在空中不散开.取重力加速度g =10 m/s2,不计空气阻力.求水流稳定后在空中有多少立方米的水.
答案 2.4×10-4 m3
解析 以t表示水由喷口处到落地所用的时间,有:h = gt2 ①
gt2 ①
单位时间由喷出的水量Q = Sv ②
空中水的总量应为:V= Qt ③
由以上各式得:V= S·v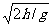 ④
④
代入数值得:V=2.4×10-4 m3
8. (05·上海·10)如图所示的塔吊臂上有一可以沿水平方向运动的小车A,小车下装
(05·上海·10)如图所示的塔吊臂上有一可以沿水平方向运动的小车A,小车下装
有吊着物体B的吊钩,在小车A与物体B以相同的水平速度沿吊臂方向匀速运
动的同时,吊钩将物体B向上吊起,A、B之间的距离以d =H - 2t2(SI)(SI表
示国际单位制,式中H为吊臂离地面的高度)规律变化,则物体做 ( )
A.速度大小不变的曲线运动 ?B.速度大小增加的曲线运动
C.加速度大小方向均不变的曲线运动 ?D.加速度大小方向均变化的曲线运动
答案 BC
解析 B物体参与了两个运动,一个是水平方向的匀速运动,另一个是在竖直方向上的运动,由d =H-2t2可知,A、B之间距离匀加速减小,且加速度a=4 m/s2,因此B在竖直方向上做匀加速运动,两个运动的合成为匀加速曲线运动.
7.(06上海理综12)“时空之旅”飞车表演时,演员驾着摩托车,在球形金属网内壁
上下盘旋,令人惊叹不已,摩托车沿图示竖直轨道做圆周运动的过程中 ( )
 A.机械能一定守恒
?
A.机械能一定守恒
?
B.其输出功率始终保持恒定
C.经过最低点时的向心力仅由支持力提供 ?
D.通过最高点时的最小速度与球形金属网直径有关
答案 D
解析
摩托车在竖直轨道做圆周运动的过程中,摩擦力、发动机的动力都要做功,机械能不守恒;摩托车在运动过程中,其受力情况和运动情况不断变化,其输出功率发生变化;在最低点时向心力由重力和支持力来提供;通过最高点时,满足最小速度时的向心力仅由重力提供,即:mg= ,故D项正确.
,故D项正确.
6.(06·重庆理综·14)如图所示,在同一竖直面内,小球a、b从高度不同的两点,分别以初速度va和vb沿水平方向抛出,经过时间ta和tb后落到与两抛出点水平距离相等的P点.若不计空气阻力,下列关系式正确的是 ( )
 A.ta>tb,va<vb
A.ta>tb,va<vb
B.ta>tb,va>vb
C.ta<tb,va<vb ?
D.ta<tb,va>vb
答案 ?A?
解析 两小球做平抛运动,由图知ha>hb,则ta>tb;又水平位移相同,根据s =vt,可知va<vb.
5. (04·全国卷Ⅲ· 20)如图所示,轻杆的一端有一个小球,另一端有光滑的固定轴O,现给球一初速度,使球和杆一起绕O轴在竖直面内转动,不计空气阻力,用F表示球到达最高点时杆对小球的作用力,则F ( )
(04·全国卷Ⅲ· 20)如图所示,轻杆的一端有一个小球,另一端有光滑的固定轴O,现给球一初速度,使球和杆一起绕O轴在竖直面内转动,不计空气阻力,用F表示球到达最高点时杆对小球的作用力,则F ( )
A.一定是拉力
B.一定是推力
C.一定等于零
D.可能是拉力,可能是推力,也可能等于零
答案?D
解析
最高点球受重力mg与杆的作用力F,由牛顿第二定律知mg+F=ma向=m (v为球在最高点的速度,R为球做圆周运动的半径)当v=
(v为球在最高点的速度,R为球做圆周运动的半径)当v= 时,F=0;当v>
时,F=0;当v> 时,F>0,即拉力;当v<
时,F>0,即拉力;当v< 时,F<0,即推力.故D对.
时,F<0,即推力.故D对.
4.(06·天津理综·16)在平坦的垒球运动场上,击球手挥动球棒将垒球水平击出,垒球飞行一段时间后落地.若不计空气阻力,则 ( )
A.垒球落地时瞬时速度的大小仅由初速度决定
B.垒球落地时瞬时速度的方向仅由击球点离地面的高度决定
C.垒球在空中运动的水平位移仅由初速度决定
D.垒球在空中运动的时间仅由击球点离地面的高度决定
答案 D?
解析 垒球落地时瞬时速度的大小是v= ,其速度方向与水平方向的夹角满足:tanα=
,其速度方向与水平方向的夹角满足:tanα= ,由此可知,A、B错;垒球在空中运动的水平位移s = v0t = v0
,由此可知,A、B错;垒球在空中运动的水平位移s = v0t = v0 ,故C错;垒球在空中运动的时间t=
,故C错;垒球在空中运动的时间t= ,故D对.
,故D对.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com