2．下图是甲、乙、丙三种生物体细胞内染色体情况示意图，则对应的基因型可依次为(　　 )

A．AaBb，AAaBbb，Aaaa

B．AaaaBBbb，Aaa，ABcd

C．AAaaBbbb，．AaaBBb，AaBb

D．AaaBbb，AAabbb，ABCD

1．细胞的有丝分裂和减数分裂都可能产生可遗传的变异，其中仅发生在减数分裂过程的变异是 (　　 )

A．染色体不分离或不能移向两极，导致染色体数目变异

B．染色体复制时受诱变因素影响，导致基因突变

C．非同源染色体自由组合，导致基因重组

D．非同源染色体某片段移接，导致染色体结构变异

12、题中导线通电后，棒受安培力的冲量，使它获得初速度，设通通电电时间为，由动量定理得　 (1)　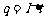 　(2)棒刚好到最高点有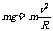：　 (3)　 由机械能守恒定律得： 　(4)可求q=5C

11、作出反粒子在磁场中运动的轨迹如图所示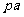，圆心在O₁.轨迹半径R_1=.=.

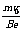反氚核的轨道半径R₂=，而R₂=rtanα,α=60⁰.所以应打在b点，偏转角即为60⁰

10、(1)如图所示

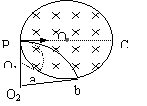(2)初始时刻小球受的洛伦兹力为＞mg故小球在摩擦力作用下做减速运动，细管在摩擦力作用下做加速运动，设小球与细管最终速度相同，都为v₁,由动量守恒得：v_`=4m/s,由小球竖直方向受力平衡，则小球与细管的弹力大小为N=F-mg=qv_球B-m_球g，由上式知，由于v_球不断减小，N也将减小，当N=0时，摩擦力消失.小球与细管就此做匀速运动，设此小球速度为v₂,有Bqv₂=mg,得v₂=10m/s.由于v₂＞v₁，可见小球速度减到10m/s时系统将稳定运动，设此时细管速度为v,由动量守恒定律得v=2.5m/s. 由能量守恒定律得

Q==13.75J

9、(1)　 (2)t=6.5T=4.1s

1、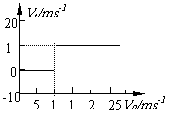C　 2、CD　 3、AB　 4、ACD　 5、C　 6、AD 7、CD　 8、AB　

3．2　 磁　 场

例1、设粒子在磁场中做圆周运动的半径为R，则有　 qv₀B=m　 ①圆心在过A与v₀方向垂直的直线上，它到A点距离为R，如图所示，图中直线AD是圆轨道的弦，故有∠OAD=∠ODA，用γ表示此角度，由几何关系知　 2Rcosγ=AD　　 ② dcosβ=AD　　 ③ α+β+γ=π/5　 ④　 解②③④得R=⑤代入①得B=⑥

例2、(1)r_m=2×10^-2m　 (2)该电子运动轨迹圆心板H处、恰能击中B板M处．随着电子速度的减小，电子轨迹半径也逐渐减小．击中B板的电子与Q点最远处相切于N点，此时电子的轨迹半径为d，并恰能落在下板上H处．所以电子击中B板MN区域和A板PH区域．在△MFH中　 FH=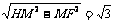

QM=PF=(2-)d=2.68×10^-3m　 ON=d=1×10^-2m　 PH=2d=2×10^-2m电子能击中B板Q点右侧与Q点相距2.68×10^-3m─1×10^-2m的范围．电子能击中A板P点右侧与P点相距0─1×10^-2m范围．

(3)要使P点发出的电子能击中Q点，则有r=mv/Be　 rsinθ=d/2　 解得　 vsinθ=8×10⁶　 v取最大速度　　 3.2×10⁷m/s时，sinθ=1/4,θ_nim=arcsin1/4　　 v取最小速度时θ_max=π/2　　 v_nim=8×10⁶m/s,所以电子速度与θ之间应满足vsinθ=8×10⁶　 且θ∈[arcsin1/4, π/2]　 v∈[8×10⁶m/s, 3.2×10⁷m/s]

例3、

例4、(1)由于碰撞时速度v与边垂直，粒子运动轨迹的圆心一定位于三角形的边上，粒子绕过三角形顶点DEF时的圆心就一定要在相邻边的交点(即DEF)上，粒子从S点开始向左做圆周运动，其轨迹为一系列半径为R的半圆，在SD边上最后一次的碰撞点与D点的距离应为R，所以SD的长度应是R的奇数倍，即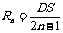(n=1,2,3…)粒子从FE边绕过E点转回到S点时，情况类似，即DE长度也是轨道半径的奇数倍，即DE=(2K-1)R_K．又因为DE=3DS，因此为使粒子与三角形各边发生垂直碰撞，R必须满足下面的条件：R_n=(n=1,2,3…),此时SE=3DS=(6n-3)R_n(n=1,2,3…),SE为R_N的奇数倍的条件自然也满足，只要粒子绕过D点与FD相碰，由对称性关系可知，以后的碰撞都能与三角形边垂直．

根据牛顿第二定律，有Bqv=mv²/R_n,得v_n=-BqR_n/m　 所以v_n=(n=1,2,3…)　 ①

(2)这些粒子在磁场中运动时，由式①可知v_n越大，n取值越小，其最小值为n=1，

那么此种情况下粒子与边碰撞的次数最少，而T=2πm/Bq,故经历时间也愈小，如

图所示，由图可看出该粒子的轨迹包括3×1个半圆和3个圆心角为300⁰圆弧，

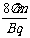
练习题

12．两根相距L=2m的光滑光滑平行直导线，左端接有电源，右端连接着半径R=0．5m的光滑圆弧形导轨，在导轨上垂直搁置一根质量m=0．1kg的金属棒，整个装置处于竖直向上，磁感强度为0．1T的匀强磁场中，当在棒中通以如图3-2-10所示方向的瞬时电流时，金属棒受到安培力作用从静止起向右滑动刚好能达到圆弧轨道滑动，刚好能达到圆弧轨道的最高点，求通电过程中通过金属棒的电量．(取g=10m/s²)

11．1998年6月2日，我国科学家研制的阿尔法磁谱仪由“发现号”航天飞机搭载升空，用于探测宇宙中的反物质和暗物质(即反粒子)--，如₁³H反粒子_-1³H．该磁谱仪核心部分截面区域是半径为r的圆形磁场，P为入射窗口，各粒子从P射入速度相同，均直径方向，Pabcde为圆周上等分点，如反质子射入后打在a点，则反氘核粒子射入将打在何处，具偏转角多少？

	B